INTRODUCTION
Bifidobacteria is indicated to affect the gastrointestinal health of humans and animals significantly. Numerous intensive studies have been conducted on gut health in relation to these bacteria [1]. These studies have enabled the use of bifidobacteria as probiotic strains, which are live beneficial microflora orally administered to humans for their dominance in the intestine.
The third commonly used genus in probiotics application, bifidobacteria were first used by Mayer in 1949 in making baby food. Later in 1968, Schuler Malyoth and his colleague showed that this bacterium can also be cultivated in dairy products [1], and the bacteria gained importance in the industry due to many health benefits. For only a few past decades, hundreds of bifidobacteria-containing foods have been produced and made available under trademarks worldwide [2].
One of the widest uses of bifidobacteria in probiotic products is their inclusion in dairy products that have been historically consumed by humans [3]. Regarding this, Bifidobacterium animalis subsp. lactis is the most widely used Bifidobacterium species. They appear in various arrays of dietary supplements and foods, especially fermented milk and junk foods. This organism is also considered the organism of choice technologically due to the high survival ability in the human gastrointestinal tract, and better feasibility compared to other bifidobacteria [4–7]. Therefore, it is important that we cultivate B. animalis subsp. lactis on a large-scale for manufacturing.
Bifidobacterium animalis subsp. lactis is possibly the best-known of the Bifidobacterium family, which requires nutrition media containing numerous amino acids, vitamins and related growth factors, for instance low oxidation and miner components [8]. Although various bifidobacteria growth media has been studied, these are unsuitable for large-scale production due to low cell mass production, unavailable materials, complex process, cost, and difficult harvesting problems [1,8,9]. Therefore, prevalent commercial media, which can limit the defects of previous ones, are required.
Yeast extract - Soy Peptone - Glucose (YPG) medium is considered a nutrient medium with rich amino acid and carbohydrate deposits [10], and with the addition of growth stimulated factors such as L-cysteine and Ferrous sulfate, YPG meets the requirements for the production of mass cell concentrations of bifidobacteria. Moreover, by using inexpensive materials, a new medium should be cost-effective and feasible during manufacturing.
Besides, one of the major components in designing new fermentation media is numerous experiments. Response surface methodology (RSM) is a collection of statistical and mathematical techniques including factual designs and regression analysis, which is more suitable for accessing multifactor experiments [11–13]. Therefore, using RSM provides a unique solution to determine the optimized growth conditions of Bifidobacterium in YPG medium.
This study outlines the optimized mass cell production of B. animalis subsp. lactis JNU306 in Yeast extract-Peptone Soy-Glucose -based medium using RSM.
MATERIALS AND METHODS
Bifidobacterium animalis subsp. lactis strain JNU306 was originally isolated from infant feces and used as a freeze storage strain at Chonnam National University. The Skim Milk medium [14] and blood-liver (BL) medium [15] were used as storage and activation media, respectively, for B. animalis subsp. lactis JNU306. This strain was stored at −70°C. The bacterium was activated by inoculating a colony in BL medium anaerobically at 37°C for 48 h. The strain was further propagated by incubating twice in BL broth to obtain a biomass concentration of 108 CFU/mL. To limit the carryover of the previous medium, the culture was centrifuged at 3,000 rpm for 15 min at 4°C to harvest cells, and the cells were resuspended in the same medium before incubating (0.1%) in various media.
The test media components used in the experiment comprised yeast extract (HY-YEST 501, Kerry bioscience, Beloit, WA, USA), peptone soy (Peptone S, Daejung, Siheung, Korea), glucose (D[+]-glucose, Junsei, Tokyo, Japan), L-cysteine (L-cysteine hydrochloride monohydrate, Sigma, St. Louis, MO, USA) and ferrous sulfate (Iron (II) Sulfate, Wako, Richmond, VA, USA). The media were autoclaved at 121°C for 15 minutes and cooled to room temperature before inoculation with cell pellets. The culture was incubated in 50-mL screw cap glass tubes (Cole-Parmer, Montreal, QC, Canada) containing 30 mL of broth and 5 mL of paraffin liquid to create an anaerobic environment. The fermentation was conducted in a water bath at 37°C for 24 h and at pH 7.0–7.2.
Viable cell enumeration was performed by diluting samples several times in a buffered saline solution containing (in g/L): potassium phosphate monobasic 4.5; sodium phosphate dibasic, 6; L-cysteine, 0.5, and Tween 80, 0.5. The resulting mixture was stirred using a magnetic stirrer until absolute homogenization to give a 10-fold dilution (wet weight/volume). Aliquots (1 mL) of each dilution were evenly spread on plates of freshly prepared BL media. Plates were incubated at 37°C for 48 h by both methods of anaerobic jars and steel wool in anaerobic incubator (Anarorator, Hanteck, Uiwang, Korea) and anaerobic packs (AnaeroPack, Mitsubishi Gas Chemical, Tokyo, Japan).
The culture medium was incubated after various treatment combinations under anaerobic conditions at 37°C for 24 h. After incubation, the number of viable cells was estimated by plate counting. Bacterial growth was tested with 30 mL volumes of medium in a 50-mL tube. For the factors for our response surface experiment, peptone soy, yeast extract, glucose, L-cysteine, and ferrous sulfate were selected. As our response surface design, the five-level-five-factor central composite design (CCD) was chosen. Table 1 displays the factors and their levels in our CCD. Table 2 shows our CCD, which consists of 32 factorial, 10 axial, and 6 center runs, and the responses from these 48 runs. The responses represent maximum biomass counts at 24 h. With Log 10 CFU/mL as their unit, the responses ranged from 7.99 to 10.29.
RESULTS
First, the second-order polynomial regression model was used to model the experimental data in Table 2. However, this model turned out to be inadequate, as indicated by the analysis of variance (Table 3); the model was non-significant (p = 0.1116 > 0.05), the r2 was low (r2 = 0.5501), and the lack of fit was significant (p = 0.0032 < 0.05).
| Residual | DF | Sum of squares | Mean square | F-value | p-value |
|---|---|---|---|---|---|
| Lack of fit | 22 | 2.225909 | 0.101178 | 15.48 | 0.0032 |
| Pure error | 5 | 0.032683 | 0.006537 | ||
| Total error | 27 | 2.258593 | 0.083652 |
Next, the following trials were made for improving the second-order model. First, cubic terms were added to the second-order model, but this did not enhance the model. Second, three-way interaction terms were added to the second-order model, yet, the improvement made by this attempt was insufficient. Third, three-way and four-way interaction terms were added to the second-order model, and this augmented model turned out to be satisfactory (Table 4), as displayed by the ANOVA; the model was significant (p = 0.0001 < 0.05), the r2 was high (r2 = 0.9646), and the lack of fit was nonsignificant (p = 0.1110 > 0.05). Thus, this model, with 5 linear, 5 quadratic, 10 two-way interaction, 10 three-way interaction, and 5 four-way interaction terms as its explanatory variables, was selected as the final model. The coefficients in this final model are indicated in Table 5.
| Residual | DF | Sum of squares | Mean square | F-value | p-value |
|---|---|---|---|---|---|
| Lack of fit | 7 | 0.145237 | 0.020748 | 3.17 | 0.1110 |
| Pure error | 5 | 0.032683 | 0.006537 | ||
| Total error | 12 | 0.177921 | 0.014827 |
Through a search on a grid [17], we maximized the predicted response from the model having the coefficients in Table 5. The bounds for the factor levels were , because the radius of the spherical region of the experimental design displayed in Table 2 was Thus, with the intervals of , we made a search within the spherical region having the radius of for which the constraint was . This search, which was conducted using SAS data-step programming, determined the optimum point described in Table 6, which states the estimated maximum of the response (Logs10 CFU/mL) as 10.265.
A plot of response surface contours was drawn for two of the five factors; the vertical axis and the two horizontal axes represented the response predicted from the model and the actual levels of the two explanatory factors, respectively. Fig. 1 contains all 10 such plots. In each plot, the factors not represented by the two horizontal axes are fixed at their optimum actual levels.
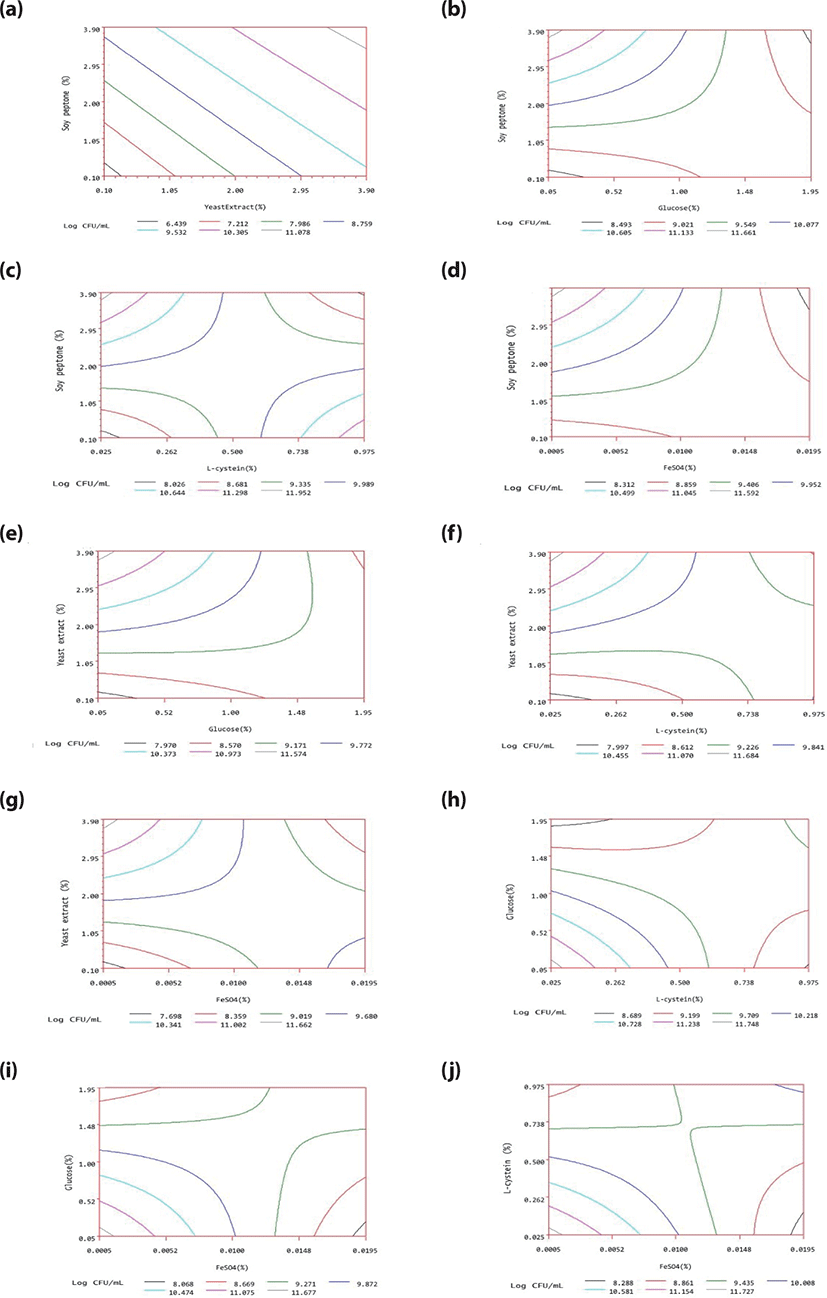
To measure the adequacy of the model (Table 7), a validation experiment was performed at the optimum point of 2.8791% yeast extract, 2.8030% peptone soy, 0.6196% glucose, 0.2823% L-cysteine, and 0.0055% ferrous sulfate, to verify the validity of the optimum medium. Besides, to assess the application potential in manufacturing, it was appropriate to test the mass cell- producing ability of several organism strains as well as assess the economical optimization of the medium. Therefore, three bifidobacterial strains including B. longum ATCC 15907, B. bifidum ATCC 35914 and B. aminalis subsp. lactis BB12 were used in cell count evaluation as well.
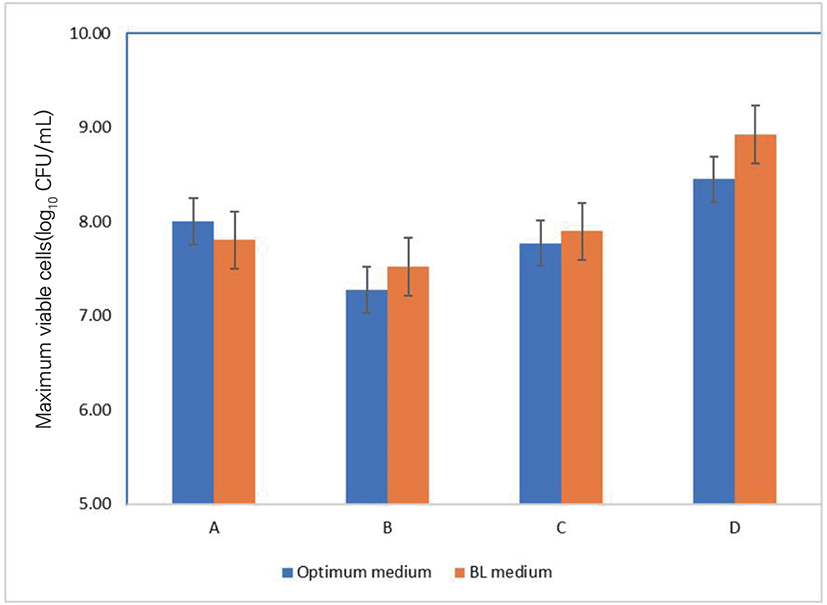
The maximum biomass production at 20 h incubation of bifidobacteria strains was expressed via Fig. 2 and the economical-effect of optimum medium was calculated and shown in Table 7. Fig. 2 showed that in the two media, the numbers of viable cells of all bacterial strains after a 20 h-incubation were similar and there were no concrete differences between the two media. Moreover, the price for producing 250 liters of the media was ≥ $100 US dollars less than the same volume of the BL broth; the new medium costs 79.04% the price of the BL medium (Table 7).
DISCUSSION
In a similar research to optimize growth conditions of Bifidobacterium pseudocatenulatum G4, a candidate probiotic organism achieved a maximum biomass production of 9.129 Log 10 CFU/mL [9]. Hussain et al. [17] recently reported on the optimal growth conditions of B. bifidum in small scale fermentation, and observed the maximum wet-cell weight at optimized growth condition was 34.1 g/L. The final viable cells increased to 9.398 Log 10 CFU/mL under constant pH condition.
Besides, many intensive studies have been conducted on aspect finding optimized medium for maximum biomass production of many different bacterial species via different parameters such as viable cells Log 10 CFU/mL [9,18,19], maximum specific growth rate per hour [20] or dry cell weight, gram per liter [21]. Thus, in comparison with these published papers, the result of this study is limited. Furthermore, since growth performance is a specific strain, which was very popularly used in manufacturing the optimum medium should be compared on commonly used commercial media with the individual strain.
To test the mass cell-producing ability of several bacterial strains, the maximum biomass obtained from the optimized medium was compared with growth performance in BL broth, which is frequently used as optimal medium [15].
In the two media, the numbers of viable cells of all bacteria were similar and there were no practical differences between the two media. These results suggested the applicability of the optimum medium. Moreover, the cost of the new medium is lower than that of BL medium. These results confirmed that our new optimum medium has potential application in manufacture.
CONCLUSIONS
The use of a new response surface approach as a statistical tool to improve the growth of B. animalis subsp. lactis strain JNU306 within yeast extract, soy-peptone, glucose, L-cysteine, and ferrous sulfate components has been demonstrated in this study. This work has developed a statistical model to assess the third-order polynomial effects between components and established their estimated optimum levels to maximize biomass production. One of the highest viable cell counts was observed: the optimum point was 2.8791% yeast extract, 2.8030% soy-peptone, 0.6196% glucose, 0.2823% L-cysteine, and 0.0055% ferrous sulfate. Through a validation experiment, the optimum medium turned out to be economically viable in that its cultivation amount was the same but production was more cost-effective than BL medium.
