Background
Rice-cool season forage crop rotation system in paddy field is popular in East Asia, including Korea [1,2]. Based on the actual farming situation in 2017, an area of 755,000 ha was used as a paddy field [3]. Italian ryegrass (Lolium multiflorum Lam., IRG) cultivation area in the paddy field was 134,880 ha in 2015, which was 52.0% of the total productivity of forage crops in the Korea [4]. The IRG grows well in paddy fields due to its high moisture resistance and widespread roots. In particular, the growing period might be insufficient by the rotation system in paddy fields [5]. Therefore, we focused on the paddy field, which was an important environmental condition for the survival of IRG cultivation in East Asia. Many studies related to soil biochemical, physical, topographical and geological properties have been carried out in paddy field. Soil classification and survey are important for fostering sustainable agricultural development [6] and selection of cultivars [7]. After the soil classification was carried out by Rural Development Administration (RDA), then the soil-environment information system was developted and released in the Korea. The soil physical properties from the system were provided by ordinal categorical information with mapping. In this study, the soil physical measurements were considered to identify its causality with climates for IRG yield in paddy field.
The IRG yield is sensitive to the variability of climates before and after winter, which indicates the importance of climatic data is stand out nowadays. Climate data assessment is critical to ensure that many data users have access to all the climate information needed to assess climate change and variablity, as well as providing various climate services [8]. In particular, the assessment of climate big data in this study, such as causality identification, was important in selecting climatic variables, identifying associations between climatic variables and organizing pathaways. Climate big data from the weather information system of Korea Meteorological Administration (KMA) have been widely used in agricultural science. In order to conduct IRG yield prediction with climate big data, a model was developed using location-based climatic variables and evaluated through cross-validation method [9,10]. They reported that homogeneity was necessary to decrease the variance in historical data due to quite different characteristics by location. As a way of yield prediction study, the predicted IRG yield was mapped to the major cultivation locations with mapping related to climatic variables by a location through the geographic information system, and the model also was evaluated was used in terms of climate suitability assessment [11]. As a result, the error of the predicted value ranged from minimum 1.7% to maximum 8.4% depeing on the location.. In general, climate big data includes many variables, but simple structural models are difficult to handle its effects. Thus various analytical methods have been used to reflect the complex effects such as covariance, neural networks model and structural equation model (SEM) nowadays.
Since frequent use of applications based on big data, several powerful analytical techniques have been developed for specific proposals. SEM has been carried out through two steps, which consists of measurement and structural parts [12,13]. First, the number of variables in the measurement part have effectively reduced to some common factors to prevent an excessive increase in the number of parameters. Next, the paths to verify direct, indirect and mediate effects, have been set up to establish a network between common factors in the structural part. That is, the measurement and structural parts represent the same performance of factor and path analysis, respectively. Therefore, SEM should be performed with the multivariate normality assumption as multivariate data analysis [14]. The continuous quantitative scale is suitable for analyzing in SEM, therefore, the ordinal scale is not continuous quantitative and should not be treated as if they are because it does not have origins or measurements units [15]. Causality by SEM provides the ability to check the flow of the effects between factors and can play a role in presenting the possibility of experimenting in the real world [16]. It is important to identify the causality in a natural ecosystem since more complicated and various factors than those commonly known in crop and environmental science affect the growth and development of crops [17,18]. Because of the advantages of considering the complicated situation of SEM, SEM is used not only from an ecological perspective that emphasizes environmental flow but also from a physiological perspective that emphasizes the flow of crop itself. Zhang et al. [19] reported that the crop phenology, canopy traits, yield were included to check how these characteristics related to seed yield in a phenotypically diverse collection of flax germplasm in SEM. The effects of seeding date and irrigation timing on yield were confirmed via SEM in terms of cultivation management [20]. In the environmental relationship between climates and IRG yield, the prototyped structure was generated that takes into account temperature, precipitation and sunshine duration in autumn and next spring [21]. As a result, IRG yield was directly affected by spring temperature and indirectly affected by the spring precipitation through other factors. This causality of climates was used to simulate the causality between climates and forage barley (Secale cereale L.) yield as prior information of the Bayesian approach [22]. The climate information from the prototyped IRG model could be used as good prior information in cases of a small sample of cool-season forage crops. Causality of both climatic and soil factors on yield were identified initially by SEM for whole crop rye (Secale cereale L.) [23]. They found that the variation of precipitation was significally effective under the range of high temperature.
This study aimed to identify the causality of climatic and soil factors on IRG yield in the paddy field via SEM based on climate and soil big data in the Korea.
Materials and Methods
The dataset consisted of forage, climate and soil data. First, the raw forage data (n = 133) were gathered from reports of the adaptability test of imported varieties of forage crops by National Agricultural Cooperative Federation from 1992 to 2013 (22 years) as metadata. Dry matter yield, cultivars, cultivation location, year, seeding and harvesting dates were measured according to the same method and research goal. Second, the raw climate big data were collected from the weather information system of the KMA, which contains daily temperature, precipitation and duration sunshine according to cultivated year and address. Finally, the raw soil big data were collected from the soil-environment information system of RDA, which contains effective soil depth, slope, drainage classes and gravel content based on address.
After these data were merged, various variables were generated to analyze the causality: First, climatic variables were autumnal growing days (AGD, day), autumnal accumulated temperature (AAT, °C), spring growing days (SGD, day), spring accumulated temperature (SAT, °C), spring amount of precipitation (SAP, mm), spring days of precipitation (SDP, day). Second, soil physical variables were effective soil depth (ED, scale of 1 to 4, 1: 0–20 cm, 2: 20–50 cm, 3: 50–100 cm, 4: over 100 cm), slope (SL, scale of 1–6, 1: 0%–2%, 2: 2%–7%, 3: 7%–15%, 4: 15%–30%, 5: 30%–60%, 6: over 60%), drainage classes (DC, scale of 1–6, 1: somewhat excessively, 2: well, 3: moderately well, 4: somewhat poorly, 5: poorly, 6: very poorly), gravel content (GC, scale of 1–6, 1: less 0.01%, 2: 0.01%–0.1%, 3: 0.1%–3.0%, 4: 3%–15%, 5: 15%–90%, 6: over 90%). Final, forage yield variables were dry matter yield (DMY, kg/ha) and fresh matter yield (FMY, kg/ha).
In this study, the soil variables were recorded on the ordinal scale initially, thus we tried to adjust the scale through transformation. Unfortunately, the ordinal scale of the soil physical variables was inappropriate in SEM, which should be performed under the assumption of normality [12]. Therefore, jitter transformation was applied to change the scale from qualitative to quantitative by adding some noise as follows [24]:
where X = (DCT, SLT, EDT, GCT)T and J are the soil physical variables before and after transformation, respectively. runif( ) is a function to generate the random number under the uniform distribution as a noise, n is the length of X, a (= 0.5) is range to spread. The transformed soil physical variables were JDC, JSL, JED, and JGC.
SEM was performed to identify the causality of climatic and soil physical variables on the IRG yields in the paddy field. In general, SEM consists of two parts, the measurement part is used to reduce the variables to a common factor based on similarity, which is the same as factor analysis (1), structural part is used to identify the causality between the common factors by setting a path, which is the same as path analysis (2):
where Z = (FMYT, DMYT, AGDT, AATT, SGDT, SATT, SAPT, SDPT, JEDT, JSLT, JDCT, JGCT,)T is variables, Φ is a factor, Λ is a factor loading indicates the relationship between variable and factor, D is a longitudinal matrix indicates the seasonal effect between autumn and next spring, ξ and η are explanatory and response variables, respectively. Β and Γ are parameters between η and ξ, respectively. ε ~ N(0, Ωε) and δ ~ N(0, ψδ) are residual of measurement and structural parts, respectively. In particular, η is located both left and right terms in (2) as a mediate object. Some η are the result of the previous path and the cause of the next path at the same time, which indicates that the advantage of SEM can reflect complex relationships, unlike the regression model. All parameters were estimated by maximum likelihood method, the structure of paths was set by 5% significance level, model fitness, model parsimony and advices of forage experts. Where, goodness of fit index (GFI), comparative fit index (CFI) and normed fit index (NFI) were used to evaluate the model fitness, and parsimony GFI (PGFI), parsimony CFI (PCFI) and parsimony NFI (PNFI) were used to evaluate the model parsimony [25].
Correlation analysis and regression analysis were performed to select effective variables in SPSS 23.0 (IBM Corp., Chicago), SEM was performed in AMOS 23.0 (IBM Crop., Chicago), and jitter transformation was performed in R 3.2.4.
Results and Discussion
Mean FMY and DMY were 43,595 kg/ha and 8,855 kg/ha, respectively(Table 1). The dry matter percentage was 20.3% which was in the range of (17.79, 21.61) [1]. All variables had followed the normality assumption (|kurtosis| < 2, |skewness| < 2), furthermore, the mean and median were similar for the yield and climatic variables. In cases of small sample size (n < 300), it would be impossible to entirely disregard the bias even though the SEM was carried well out under the normality assumption [26]. For example, the JSL and JGC were somewhat skewed to 1.25 and 1.88, respectively. It is likely that IRG had been not cultivated in the paddy field with high slope and high gravel content due to the difficulty of cultivation management like a machine working. The mean SAT and SAP was greater than the median, which indicates high temperature and low precipitation amount due to occasional spring drought. According to Lee et al. [27], the spring drought showed strong periodicity in 4–6 years, and the southern area where IRG is mainly cultivated was more vulnerable to extreme drought than the middle area of the Korean Peninsula.
From the various variables, common factors were generated by effective reduction to identify an obvious causality between the climatic and soil physical variables through factor analysis (Table 2). As a result, the 12 variables were clearly reduced to the 5 factors: spring temperature, IRG yield, autumnal temperature, spring precipitation and soil physical factors. Here, the JDC and JGC were eliminated due to weak relationship to soil physical factor (|score| < 0.30). According to Chae et al. [28], not only slope and effective soil depth but also various soil physical properties were limited in the paddy field. The distribution of soil physical variables was narrow in this study, therefore, it was not sufficient to reflect its effects. In general, variable reduction causes information loss [14]. The accumulated variance was 78.05%, which indicates the information loss was around 22% when the number of the parameters was reduced from 12 to 5. Based on obvious features and not large information loss in the factor analysis, it was judged that the reduction was effective.
Based on the prototyped structure [21], from the autumnal temperature, spring temperature, spring precipitation, soil physical properties and crop yield factors, the structure measuring paddy field data was constructed to identify the causality one by one. In the first model (Fig. 1a), only temperature related factors were considered. Even though the residual interaction effects of accumulated temperature and growing days between autumn and spring were not significant, all paths were significant (p < 0.05). In particular, the direct and indirect effects on the IRG yield of autumnal temperature were 0.33 and 0.23 (= 0.62 × 0.37), respectively. Therefore, the autumnal and spring temperatures influenced yield as much as 0.56 and 0.37, respectively.
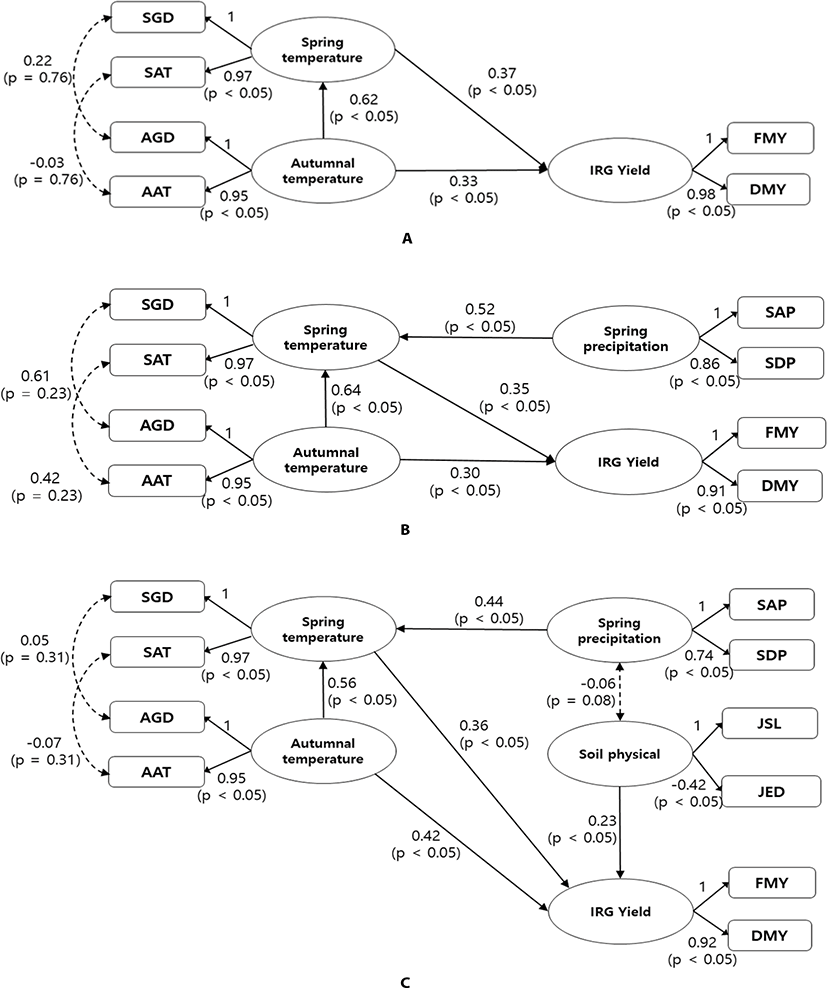
By adding spring precipitation to the first model (Fig. 1b), the spring precipitation was only linked to the spring temperature (p < 0.05), which indicates that the precipitation affected the yield through the temperature in spring growing season. As a result of correlation analysis between DMY and SAP by quartile of SAT (Table 3), the relationship became stronger as the accumulative temperature increases. In particular, the correlation between DMY and SAP was 0.70 (p < 0.05) based on over 1,507.4°C of SAT, which implies that the daily mean temperature was above 14.18°C during 106 days based on mean SGD. Therefore, we concluded that the precipitation effect on yield was effective based on sufficient temperature in the spring (14.18°C or more, at least 7.42°C or more). According to Kim et al. [23], the yield increased with increasing temperature, and the effect of precipitation on yields fluctuated significantly only at high temperature. The optimum growing temperature was in the range of 15°C–18°C, and IRG could maintain growth down to 4°C [29]. Hence, the next spring temperatures of Korea would ensure sufficient growth of IRG under stable wintering condition.
In the final model (Fig. 1c), the causality of the climatic and soil physical factors was constructed by adding the soil physical factor. The soil physical factor was related to low effective soil depth based on slope, which means good conditions to cultivate the IRG due to the wide development of the roots. According to Kristensen and Thorup-Kristensen [30], the IRG roots length, N uptake and N inflow rates were sharply shrunk at injection depths of over 0.6 m. Furthermore, IRG roots tend to widely distribute near the surface for growth and development [31]. In order of the effects on IRG yield, the autumnal temperature, spring temperature, soil physical and spring precipitation factors were 0.62 (= 0.42 + 0.56 × 0.36), 0.36, 0.23, and 0.16 (= 0.44 × 0.36). In general, the climate is easily varied year by year, while soil physical properties have changed over the long term [32]. Therefore, the impact of soil physical properties should be relatively weak comparing to the impact of temperature. In particular, the effect of temperature in autumn (0.62) was greater than that in spring (0.36). Comparing to the causality of climatic factors on IRG yield including both field types [21], the effect of spring temperature was greater than that of autumnal temperature, oppositely. It is likely that these conflicting results were caused by the differences between field types. The proportions of a sample of the upland and paddy fields were 80.5% (n = 586) and 19.5% (n = 142), respectively. Whether the IRG yield is sensitive to autumnal temperature or spring temperatures depending on whether there is a sufficient growing period in the autumn. If wintering was successful due to sufficient growing days in autumn, spring temperature contributed greatly to the IRG increases, but if not, the autumn temperature would be crucial to contribute to energy accumulation for wintering. Hence, the yield should be sensitive to autumnal temperature to cumulate the energy needed for wintering due to the lack of growing days in the paddy field. Even though the interaction between the spring precipitation and soil physical factors was not significant (p = 0.08), it does not mean no effect. Meanwhile, the effect of the spring precipitation was the lowest in this causality, which indicates that the impact of water could be weak on yield variation due to sufficient moisture content and low water dependence in the paddy.
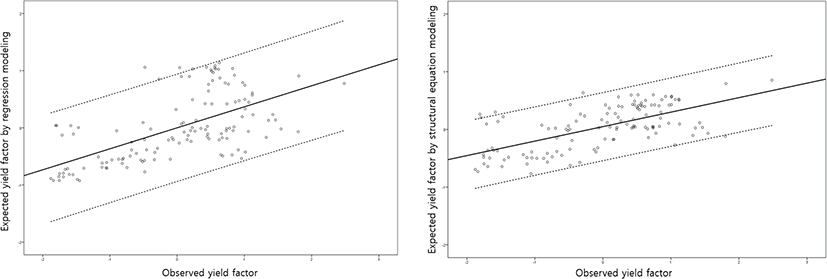
Comparing to multiple regression modeling (Table 4), only the spring precipitation effect was not significant (p = 0.92) which was similar to the direct effects by SEM. In order of effect, the spring temperature, autumnal temperature and soil physical factors were 0.33 (p < 0.05), 0.30 (p < 0.05) and 0.21 (p < 0.05), respectively. The effect of spring temperature was a little greater than that of autumnal temperature in the regression model. The contradictory result of the effect of spring temperature between SEM and regression modeling was due to the reflection of its indirect effect. The estimation of indirect effect was one of the powerful advantages of SEM to identify causality, whereas it was difficult to reflect indirect effects in regression model without some special techniques. The GFI, CFI, and NFI, which similar to R2 of the regression model [33] were 0.68, 0.78, and 0.77, respectively. For the model parsimony, the PGFI, PCFI, and PNFI were 0.39, 0.54, and 0.53, respectively. Therefore, the model fitted normally and the structure was simple [13]. In particular, the individual 95% confidence interval of the residual of SEM was narrower than that of the regression model (Fig. 2). The fitness of the regression model (R2) was 0.37, indicating a poor level. Therefore, parameters of SEM and regression model were interpreted similarly, and the SEM was better fitted to the data than the regression model, considering the applicability of indirect effects.
Conclusion
In this study, we identified the causality of climatic and soil physical factors on IRG yield in paddy field. We found the two remarkable points: the yield was sensitive to autumnal temperature due to the lack of growing days to cumulate the energy for wintering; furthermore, the effect of soil physical factor on the yield was clear while the correlation with precipitation was not significant in the paddy field. However, since the soil physical variables were categorical, thus there might be a limit to reflect its effect. This study shows that the existing structure only considering the climate was extended well by adding soil information. Therefore, we expect that the SEM measuring the environmental causality network of IRG yield will continue to expand considering more factors.
















