Comparison of accuracy of breeding value for cow from three methods in Hanwoo (Korean cattle) population

Lee, Hyo Sang; Kim, Yeongkuk; Lee, Doo Ho; Seo, Dongwon; Lee, Dong Jae; Do, Chang Hee; Dinh, Phuong Thanh N.; Ekanayake, Waruni; Lee, Kil Hwan; Yoon, Duhak; Lee, Seung Hwan; Koo, Yang Mo

doi:10.5187/jast.2023.e5

J Anim Sci Technol 2023; 65(4):720-734

pISSN: 2672-0191, eISSN: 2055-0391

DOI: https://doi.org/10.5187/jast.2023.e5

RESEARCH ARTICLE

Comparison of accuracy of breeding value for cow from three methods in Hanwoo (Korean cattle) population

Hyo Sang Lee¹^,^#

, Yeongkuk Kim²^,^#

, Doo Ho Lee³^,^#

, Dongwon Seo⁴

, Dong Jae Lee³

, Chang Hee Do⁵

, Phuong Thanh N. Dinh²

, Waruni Ekanayake³

, Kil Hwan Lee¹

, Duhak Yoon⁶

, Seung Hwan Lee³^,^*

, Yang Mo Koo¹^,^*

Author Information & Copyright ▼

¹Genetic Information Division, Korea Animal Improvement Association, Livestock Hall, Seoul 06668, Korea

²Department of Bio-AI Convergence, Chungnam National University, Daejeon 34134, Korea

³Division of Animal and Dairy Science, Chungnam National University, Daejeon 34148, Korea

⁴TNT Research Co., Anyang 14059, Korea

⁵Institute of Agricultural Science, Chungnam National University, Daejeon 34134, Korea

⁶Department of Animal Science and Biotechnology, Kyungpook National University, Sangju 37224, Korea

# These authors contributed equally to this work.

^*Corresponding author: Seung Hwan Lee, Division of Animal and Dairy Science, Chungnam National University, Daejeon 34148, Korea. Tel: +82-42-821-5772, E-mail: slee46@cnu.ac.kr

^*Corresponding author: Yang Mo Koo, Genetic Information Division, Korea Animal Improvement Association, Livestock Hall, Seoul 06668, Korea. Tel: +82-2-588-9301, E-mail: greatman009@daum.net

© Copyright 2023 Korean Society of Animal Science and Technology. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Oct 25, 2022; Revised: Jan 08, 2023; Accepted: Jan 09, 2023

Published Online: Jul 30, 2023

Abstract

In Korea, Korea Proven Bulls (KPN) program has been well-developed. Breeding and evaluation of cows are also an essential factor to increase earnings and genetic gain. This study aimed to evaluate the accuracy of cow breeding value by using three methods (pedigree index [PI], pedigree-based best linear unbiased prediction [PBLUP], and genomic-BLUP [GBLUP]). The reference population (n = 16,971) was used to estimate breeding values for 481 females as a test population. The accuracy of GBLUP was 0.63, 0.66, 0.62 and 0.63 for carcass weight (CWT), eye muscle area (EMA), back-fat thickness (BFT), and marbling score (MS), respectively. As for the PBLUP method, accuracy of prediction was 0.43 for CWT, 0.45 for EMA, 0.43 for MS, and 0.44 for BFT. Accuracy of PI method was the lowest (0.28 to 0.29 for carcass traits). The increase by approximate 20% in accuracy of GBLUP method than other methods could be because genomic information may explain Mendelian sampling error that pedigree information cannot detect. Bias can cause reducing accuracy of estimated breeding value (EBV) for selected animals. Regression coefficient between true breeding value (TBV) and GBLUP EBV, PBLUP EBV, and PI EBV were 0.78, 0.625, and 0.35, respectively for CWT. This showed that genomic EBV (GEBV) is less biased than PBLUP and PI EBV in this study. In addition, number of effective chromosome segments (M_e) statistic that indicates the independent loci is one of the important factors affecting the accuracy of BLUP. The correlation between M_e and the accuracy of GBLUP is related to the genetic relationship between reference and test population. The correlations between M_e and accuracy were −0.74 in CWT, −0.75 in EMA, −0.73 in MS, and −0.75 in BF, which were strongly negative. These results proved that the estimation of genetic ability using genomic data is the most effective, and the smaller the M_e, the higher the accuracy of EBV.

Keywords: Pedigree estimated breeding value; Pedigree index; Genomic estimated breeding value; Accuracy; Hanwoo cattle; Effective number of chromosome segments (M_e)

INTRODUCTION

The Hanwoo production system in Korea consists of three tiers, including the seed stock sector (bull selection sector), cow-calf operations, and feedlot sector [1]. The Korean government operates the bull selection program, which is called the National Genetic Evaluation Program, to select proven bulls to increase the genetic potential of the entire Hanwoo population [2]. The semen straws of selected bulls are distributed to the multiplier sector (reproduction of cows) to produce calves. The use of genetics to select bulls has gradually increased over the past 20–30 years and is remarkably successful [3]. However, no female genetic improvement program for carcass traits has been proposed. Korean farmers recognize the necessity of genetically improving the production and reproductive traits of cows to obtain higher profit margins. Compared with the bull selection breeding program, selecting females is more challenging because estimating the breeding value of a female is difficult due to a lack of information. Currently, the female estimated breeding value (EBV) can be determined for production and reproductive traits using the pedigree index (PI), bull (sire) pedigree, and best linear unbiased prediction method [4]. Pedigree data are traditionally applied to determine the EBV using phenotypes generated from half-sib, full-sib, and progeny testing [5]. However, pedigree information may be recorded incorrectly; for example, some individual identification tag numbers could be lost or incorrectly attached to livestock, leading to false pedigree information and inaccurate predictions [6]. Thus, determining an accurate EBV to select the female population during farm-level breeding operations is difficult. Farmers running small cow farms that produce calves wish to predict their cows’ EBV to obtain cows with better genetic potential; therefore, a more effective method with few errors is needed.

The disadvantages of the PI and pedigree-based best linear unbiased prediction (PBLUP) methods could be overcome by recent developments in genomic technology, which enable estimation of the genomic breeding value (GEBV) using DNA variants [7, 8]. In addition, the cost of these tests has been decreasing. Therefore, genomic information allows us to derive more accurate breeding values than previous methods [9].

The accuracy of the EBV can be affected by the genetic relatedness (genetic co-variance) between a large reference population and female candidates. The effective number of chromosome segments (M_e) is used to estimate genetic relatedness between two populations [10]. M_e is also defined as the variance of identity-by-descent among genetically related individuals [11]. The lower the M_e value, the closer the genetic relationship between the reference and test population [12]. The accuracy of the GEBV increases if the genetic relatedness between the reference and test population is high.

This study aimed to compare the accuracy of three methods (PI, PBLUP, and the genomic best linear unbiased prediction [GBLUP]) for analyzing a reference population comprised of half-sib family data and a test population (481 cows), and for identifying factors affecting the accuracy of EBVs for replacement cows for selecting females.

MATERIALS AND METHODS

Dataset

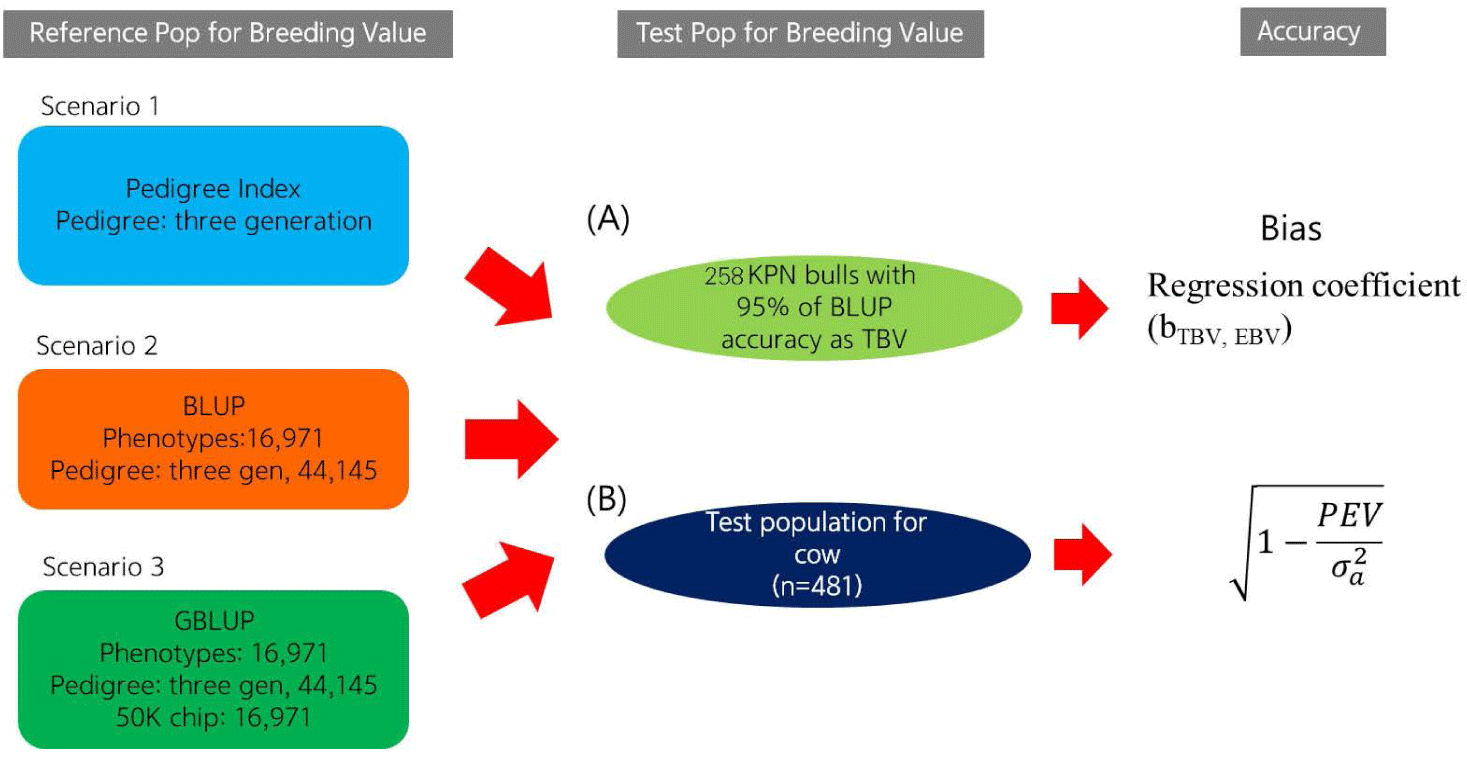
Using a reference population (n = 16,971) and female test population (n = 481), we compared the accuracy of EBVs of females estimated using different methods (Fig. 1). The reference population was comprised of 16,971 steers derived from half-sibs of 485 bulls genotyped with the Illumina bovine 50K chip (Illumina, San Diego, CA, USA). Fig. 2 describes the data collection process and shows the structure of the reference population. The phenotypes (carcass weight [CWT], eye muscle area [EMA], backfat thickness [BFT], and marbling score [MS]) for the reference population (n = 16,971) were collected from Korea Animal Products Quality Evaluation. Summary statistics of the reference phenotype are shown in Table 1. The mean and standard deviation of the CWT, EMA, BFT, and MS were 441.2 ± 50.88 kg, 95.81 ± 12.21 cm², 14.26 ± 4.92 mm, and 5.95 ± 1.85, respectively. The data were normally distributed, as shown in Fig. 3. The pedigree information for the reference population (n = 16,971) consisted of three generations including 44,145 animals (Table 2). The female herd (n = 481) was one-quarter genetically related to validate their breeding value and there were 1,595 ancestors in the pedigree (Table 3). All the female herd sample cows were selected randomly from all over the country, and derived from 104 Korea proven (KPN) bulls, and those cows are not part of the reference population. Pedigree information for the test and validation animals was collected from the Korea Animal Improvement and Association ([KAIA] https://www.aiak.or.kr/).

Fig. 1. Schematic of the breeding value accuracy using three different methods (PI, PBLUP and GBLUP). (A) 258 KPN bulls with 99% of BLUP accuracy regarded as true breeding value (TBV). (B) test population for cow with 50K genotypes. For empirical accuracy correlation TBV and EBV, theoretical accuracy using prediction error variance. KPN, Korean proven; PI, pedigree index; PBLUP, pedigree-based best linear unbiased prediction; GBLUP, genomic best linear unbiased prediction; BLUP, best linear unbiased prediction.

Download Original Figure

Fig. 2. Distribution of animals across the country and chart of KPN which is the number of progenies. (A) Distribution of reference population sampled across the country. Blue color is 23 to 26 age month, red color is 27 to 30 age month, orange color is 31 to 34 age month and gray color is less than 23 age month. (B) Number of KPN bulls (half-sib families) with different numbers of progenies in the reference population. Structure of the reference population of KPN bulls (half-sib families) based on the number of progeny in each herd. KPN, Korea proven.

Download Original Figure

Fig. 3. Distributions of the data for carcass traits of 16,971 Hanwoo reference population. (A) Carcass weight (kg), (B) Eye muscle area (cm²), (C) backfat thickness (mm), (D) marbling score (1–9).

Download Original Figure

Table 1. Descriptive summary statistics of carcass trait data in reference population (n=16,971)

Traits	Mean	SD	Minmum	Maximum
CWT (kg)	441.2	50.43	214.0	632.00
EMA (cm²)	95.82	12.07	43.00	148.00
BFT (mm)	14.2	4.77	1.00	35.00
MS	5.95	1.85	1.00	9.00
Age	30.26	1.91	21	40

CWT, carcass weight; EMA, eye muscle area; BFT, backfat thickness, MS: marbling score; Age, monthly age.

Download Excel Table

Table 2. Summary statistics of pedigree structure for reference population data (n=16,971)

Item	No. of animals (%)
Animals in pedigree	44,145 (100)
Sires	419 (0.95)
Dams	14,467 (32.77)
Animals with data	16,971 (100)
One parent unknown	8 (0.05)
Both parents unknown	2,353 (13.86)
Both parents known	14,610 (86.09)

Download Excel Table

Table 3. Summary statistics of pedigree structure for cow test population (n=481)

Item	No. of animals (%)
Animals in pedigree	1,595 (100)
Sires	93 (5.83)
Dams	481 (30.16)
Animals with data	481 (100)
One parent unknown	42 (8.73)
Both parents unknown	0 (0)
Both parents known	439 (91.26)

Download Excel Table

Quality control of 50K single nucleotide polymorphism chip data

The 481 cows were genotyped using the bovine 50K single nucleotide polymorphism (SNP) chip (Illumina). Quality control was performed while estimating the GEBVs of the 481 cows (test population) based on 16,971 commercial Hanwoo (reference population). Using Plink 1.9 software (http://pngu.mgh.harvard.edu/purcell/plink/), SNP markers with missing call rates > 0.1, minor allele frequency < 0.01, and a p-value of Hardy-Weinberg equilibrium < 0.0001 were removed [13]. A total of 40,635 SNP markers were used in this study.

Estimates of breeding values

In this study, we compared the accuracy of breeding values estimated using three different methods (PI, PBLUP, and GBLUP) for female replacement and management.

Pedigree index calculation

The National Agricultural Cooperative Federation and National Institute of Animal Science conducted performance and progeny testing to select KPN. The EBV accuracy for these bulls was 75%–80%. Based on this information, the PIs and EBVs of the test cows were estimated using a three-generation pedigree (sire, grandsire, and grand-grandsire). The equation was as follow [14]s:

P I = 12 (E B V S I R E) + 14 (E B V M a t e r n a l G R A N D S I R E) + 18 (E B V M a t e r n a l G R A N D − G R A N D S I R E)

Pedigree-based best linear unbiased prediction

A mixed model was used for PBLUP, including traits and considering the effects of environmental factors. The model was constructed using the BLUPF90 program [15,16] and has the following equation [17]:

y − X b + Z u + e

[X ′ X X ′ Z Z ′ X Z ′ Z + λ A − 1] [b^u^] = [X ′ y Z ′ y]

where y is a vector of the phenotype information; X contains the design matrix of the observations for fixed effects; b is the vector of the fixed effects, including farm, birth year, and month, slaughter year and month, and age; Z is the design matrix-matching phenotype value and random effect values; u is the vector of the random effects with a normal distribution; e is the vector of residual error effects with a normal distribution $∼ N (0, I σ e 2) . σ e 2$ is random variance, and I is the identity matrix. $λ = σ e 2 / σ a 2$ . A is the numeric relationship matrix (NRM) constructed based on the pedigree information.

Genomic best linear unbiased prediction

GBLUP uses the genomic relationship matrix (GRM) based on SNP markers. The GRM is expressed as [18].

G = M M ′ ∑ i = 1 m 2 p i (1 − p i)

Then,

Var (u) = G σ u 2

where M is the matrix for genes of individuals, m is the total number of SNP markers, and p_i is the frequency at the i-th position in the SNP.

The general linear mixed model equation for GBLUP is:

[X ′ X X ′ Z Z ′ X Z ′ Z + λ G − 1] [b^a^] = [X ′ y Z ′ y]

where Z is the incidence matrix for the animal effect (a), X is the incidence matrix for the fixed effect (b), $σ e 2$ is residual variance, and a $∼ N (0, G σ a 2) . λ = σ e 2 / σ a 2$ . Therefore, GBLUP is a BLUP that replaces NRM with G [GRM]).

Accuracy of the estimated breeding values estimated using the three methods

This study investigated the accuracy of the EBVs according to prediction error variance and the correlation between the true breeding value (TBV) and EBV. To investigate the accuracy of the EBVs derived using the three methods, we selected those of the top 258 KPN bulls (i.e., bulls with EBVs predicted by the BLUP method with 95% accuracy) as the TBVs. The Pearson’s correlation coefficients between TBV and the EBVs for the 258 KPN bulls were considered to reflect the actual accuracy.

A c c u r a c y E B V = c o r (T B V, E B V)

The accuracy of the EBVs for cows was calculated based on the prediction error variance (SE²) and additive genetic variance $σ g 2$ of the trait estimated using the BLUPF90 program [15]. The equations for the theoretical and PI EBV accuracy are as follows: [14]

A c c u r a c y P E V = 1 − S E 2 σ g 2

P I A c c = 0.25 × A c c o f E B V s i r e + 0.125 × A c c o f E B V M a t e r n a l G r a n d s i r e + 0.0625 × A c c o f E B V M a t e r n a l G r a n d − G r a n d s i r e

Calculating the number of effective chromosome segments

The genetic relatedness between the reference and test data is an important factor affecting genomic prediction accuracy that varies depending on the data set. Several methods are available to calculate the relatedness of the reference and test populations. The number of effective chromosome segments (M_e) is one of the most useful methods for calculating genetic relatedness. To determine the genetic relatedness between the reference and test populations, which affects the accuracy of the cow breeding value (EBV), we calculated M_e using genomic information [19]. Various approaches can be used to estimate M_e within a population. In this study, the following equation was used to estimate M_e [20].

M e = 1 V a r (G i j)

The genomic relationship between individuals was calculated as the covariance matrix (G_ij) [21]. In the G_ij, the variance of the covariance of the entire reference population was calculated for each individual and converted into a reciprocal number. If the variance between individual i and j was close to 0, the genetic relationship was considered weak [20]. The G_ij for the genomic relationship was estimated from M_e. In addition, we investigated the difference in prediction accuracy based on M_e.

RESULTS AND DISCUSSION

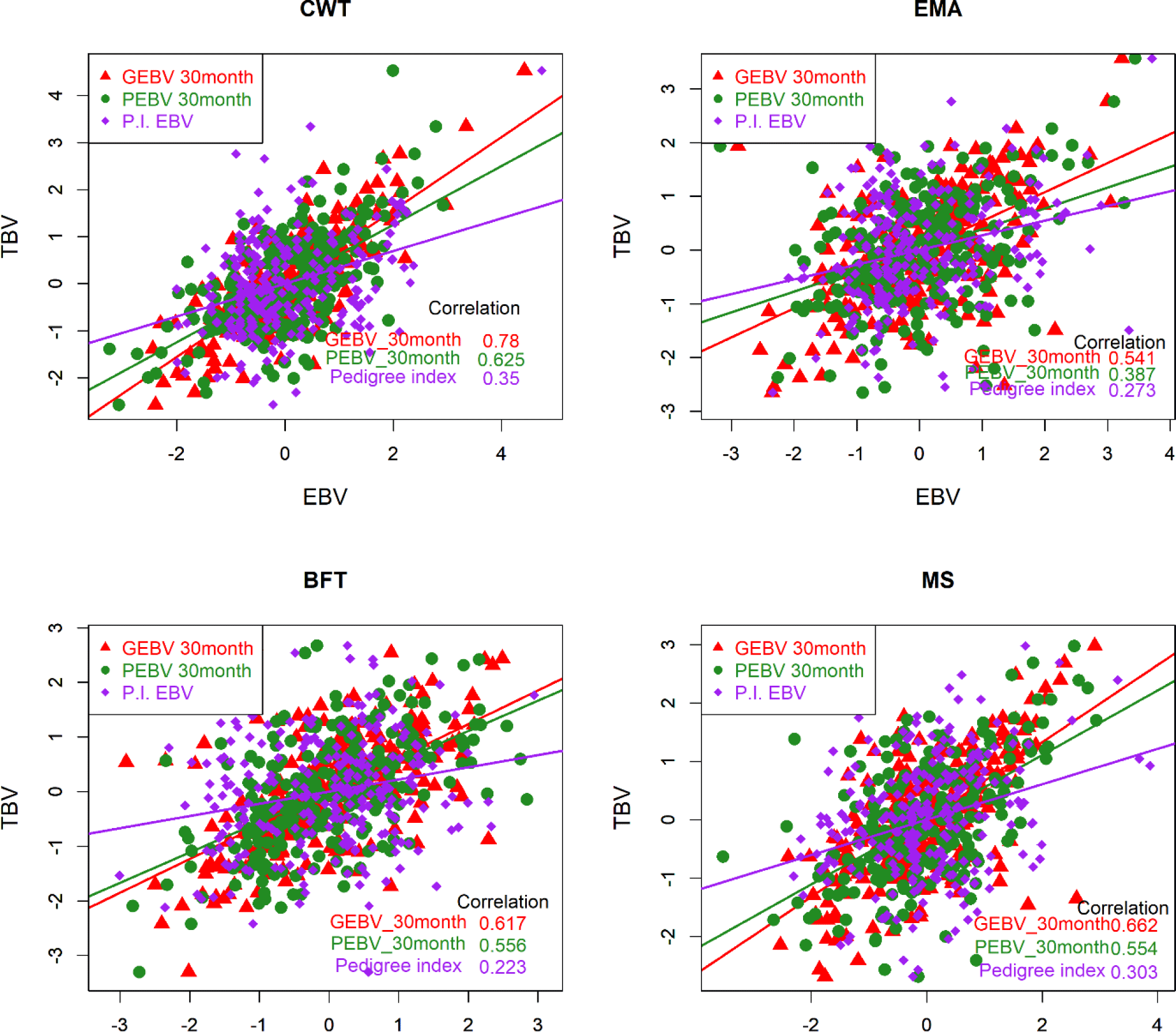
The accuracy of the EBV is ordinarily determined by two methods. Empirical accuracy is reflected in the Pearson’s correlation between TBV and EBV [22] for the three different methods, and theoretical accuracy is calculated from the prediction error variance and additive genetic variance for individual test cows [23-25]. TBV could not be determined in this study due to a lack of information on the genes controlling the phenotype. Therefore, we regarded the EBVs of the top 258 KPN bulls as TBVs to compare the accuracy of breeding values among the three different methods (PI, PBLUP, and GBLUP). The EBVs were determined for the top 258 KPN bulls and the reference population (16,971 cattle) using the three methods. Fig. 4 shows that the accuracies of GEBV were 0.78, 0.54, 0.62, and 0.66 for CWT, EMA, BFT, and MS, respectively. The PBLUP accuracies were 0.63 and 0.56 for CWT and BFT, and 0.39 and 0.56 for EMA and MS, respectively. The PI showed accuracies of 0.35, 0.27, 0.22, and 0.3 for CWT, EMA, BF, and MS, respectively. The accuracy of the GBLUP method was about 12% higher than that of the PBLUP method using pedigree information (Fig. 4). Many studies have shown that the GBLUP method is superior to PBLUP, and Naserkheil et al. [26] reported that GBLUP (single- and multiple-trait GBLUP) was approximately 19% and 36% more accurate than conventional BLUP models (single- and multiple-trait GBLUP) for carcass traits in Hanwoo. Moreover, GBLUP has performed well in many studies, and the data of the present study showed similar trends [27,28].

Fig. 4. Comparison of accuracy of genomic breeding values from three methods (PI, BLUP and GBLUP) with 16,971 phenotypic records against 258 KPNs bulls with true breeding value (we considered 95% of accuracy from BLUP as TBV). CWT, carcass weight; GEBV, genomic estimates of breeding value; PEBV, pedigree estimates of breeding value; PI, pedigree index; EMA, eye muscle area; BFT, backfat thickness; MS, marbling score; KPN, Korea proven; TBV, true breeding value.

Download Original Figure

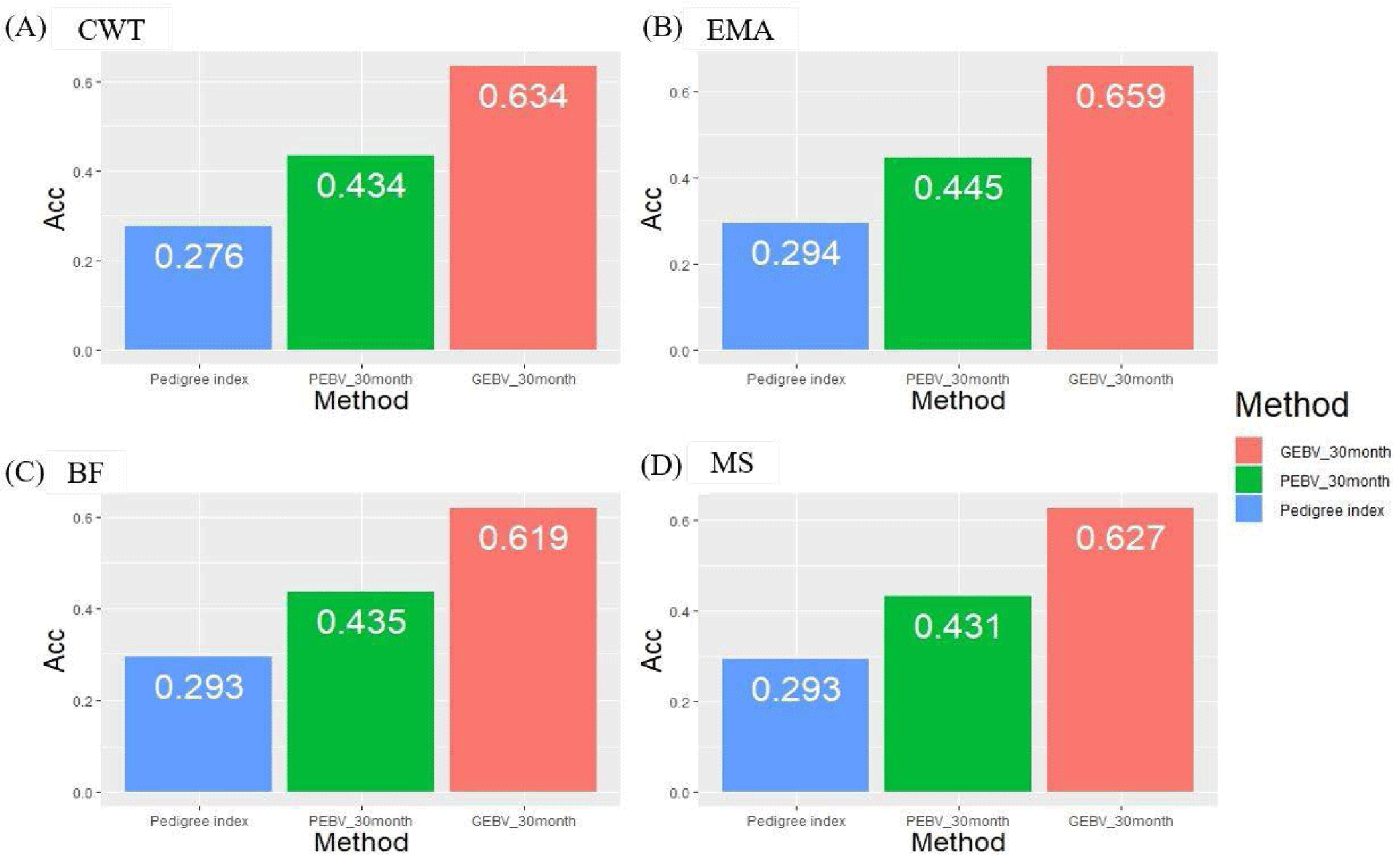
We investigated theoretical breeding value accuracy for individual test cows using prediction error variance. The breeding value of individual test cows was also estimated using the PI, PBLUP, and GBLUP methods. The reference population consisted of 416 KPN families in different age classes, and the number of progenies of each KPN half-sib family varied from 5 to 378 (Fig. 2). The accuracies of the GBLUP method were 0.634, 0.659, 0.619, and 0.627 for CWT, EMA, BF, and MS, respectively. The PBLUP accuracies were 0.434, 0.445, 0.435, and 0.431 for CWT, EMA, BF, and MS, and those for PI were 0.276, 0.294, 0.293, and 0.293, respectively (Fig. 5). The accuracy of the GEBV method was highest for all traits. The accuracies of the PBLUP EBV and PI EBV were about 0.2 and 0.35, which were lower than that of the GEBV. A difference of about 0.15 was detected between the accuracy of the PBLUP EBV and PI EBV methods.

Fig. 5. Average of theoretical accuracy using prediction error variance across all 4 traits of three methods for 481 cows. GEBV (red), estimated breeding value using genomic-BLUP; PEBV (green), estimated breeding value using pedigree-BLUP; pedigree index (blue), estimated breeding value using pedigree index. CWT, carcass weight; EMA, eye muscle area; BFT, back-fat; MS, marbling score; BLUP, best linear unbiased prediction.

Download Original Figure

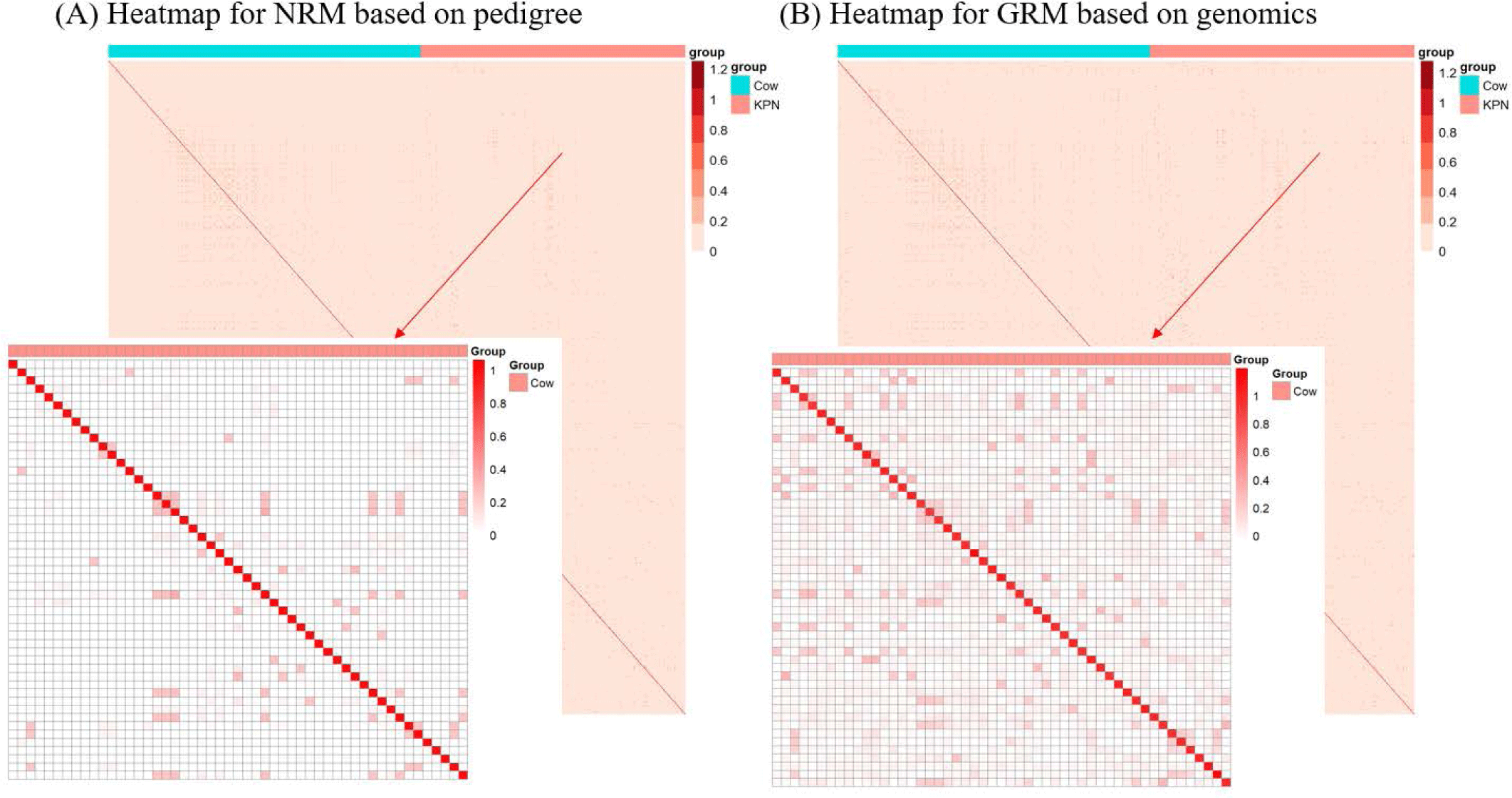
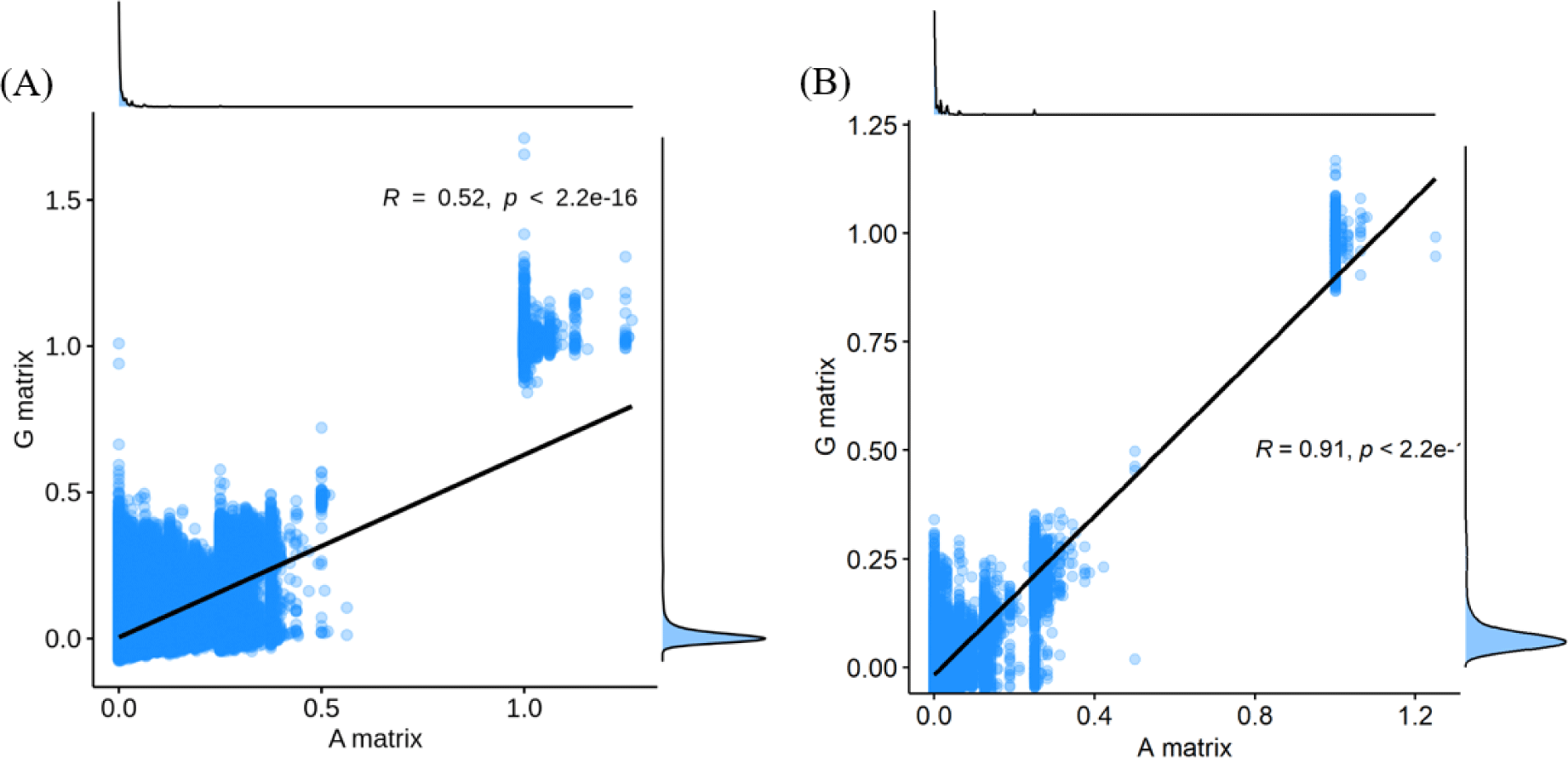
The finding that GBLUP outperformed PBLUP and PI could be explained by several factors, such as genetic covariance (genetic relatedness) between the reference and test populations [29]. In this study, a heatmap plot of the additive genetic relationships between the reference and test populations (cow) showed that, with the GRM, there was a stronger additive genetic relationship compared with pedigree-based NRM (Fig. 6). Clark et al. [29] reported that the accuracy of genomic selection depends on the strength of the relationships between the reference and test populations. If unrelated animals were estimated using the PBLUP method, accuracy would be close to zero. In contrast, the GEBV method showed high accuracy for animals that had no pedigree relationship with animals in the reference data set. The breeding values estimated using the GBLUP method were more accurate for closely related animals (~0.5) compared to those of the PBLUP and PI. Similar results were reported by Hayes et al. [30] and Habier et al. [31,32] for populations with a close relationship. Therefore, genetic relatedness is a major factor in the higher accuracy of the GBLUP compared to the PBLUP and PI seen in this study. A drawback of applying the PBLUP and PI methods to a half-sibling dataset (without individual phenotypes or progeny information) is that the accuracy of the EBV does not increase over 50% because of Mendelian sampling error [33]. This drawback cannot be solved at birth of the animal using the pedigree information [33]. Analysis of genetic gain depends on the accuracy and time taken to estimate the Mendelian sampling term. The GBLUP method is one way to control Mendelian sampling error because it provides useful information on alleles that originated from the parents. And both NRM and GRM consider an inbreeding coefficient, but GRM has more accurate inbreeding coefficient information (Fig. 7). Therefore, the GBLUP method produced more accurate breeding values than the PBLUP method in this study. The pedigree information included man-made error (affecting 10% of test animals), which caused the NRM to diverge from the actual genetic covariance. A simulation study by Nwogwugwu et al. [6] showed that a 20% pedigree information error rate led to a 5%–10% decrease in prediction accuracy.

Fig. 6. Comparison of genetic relationship of pedigree based NRM and genomic based GRM for test and ancestor (KPN) population. Red and blue group color represent ancestor (KPN; red), test data (cow; blue), respectively. Heatmap color density indicating levels of relationships was displayed. NRM, numeric relationship matrix; GRM, genomic relationship matrix; KPN, Korea proven.

Download Original Figure

Fig. 7. Comparison of genetic relationship of pedigree based NRM (A matrix) and genomic based GRM (G matrix). (A) Relationship between reference population (16,971) and test population (481). (B) Relationship of cow test population (481). NRM, numeric relationship matrix; GRM, genomic relationship matrix.

Download Original Figure

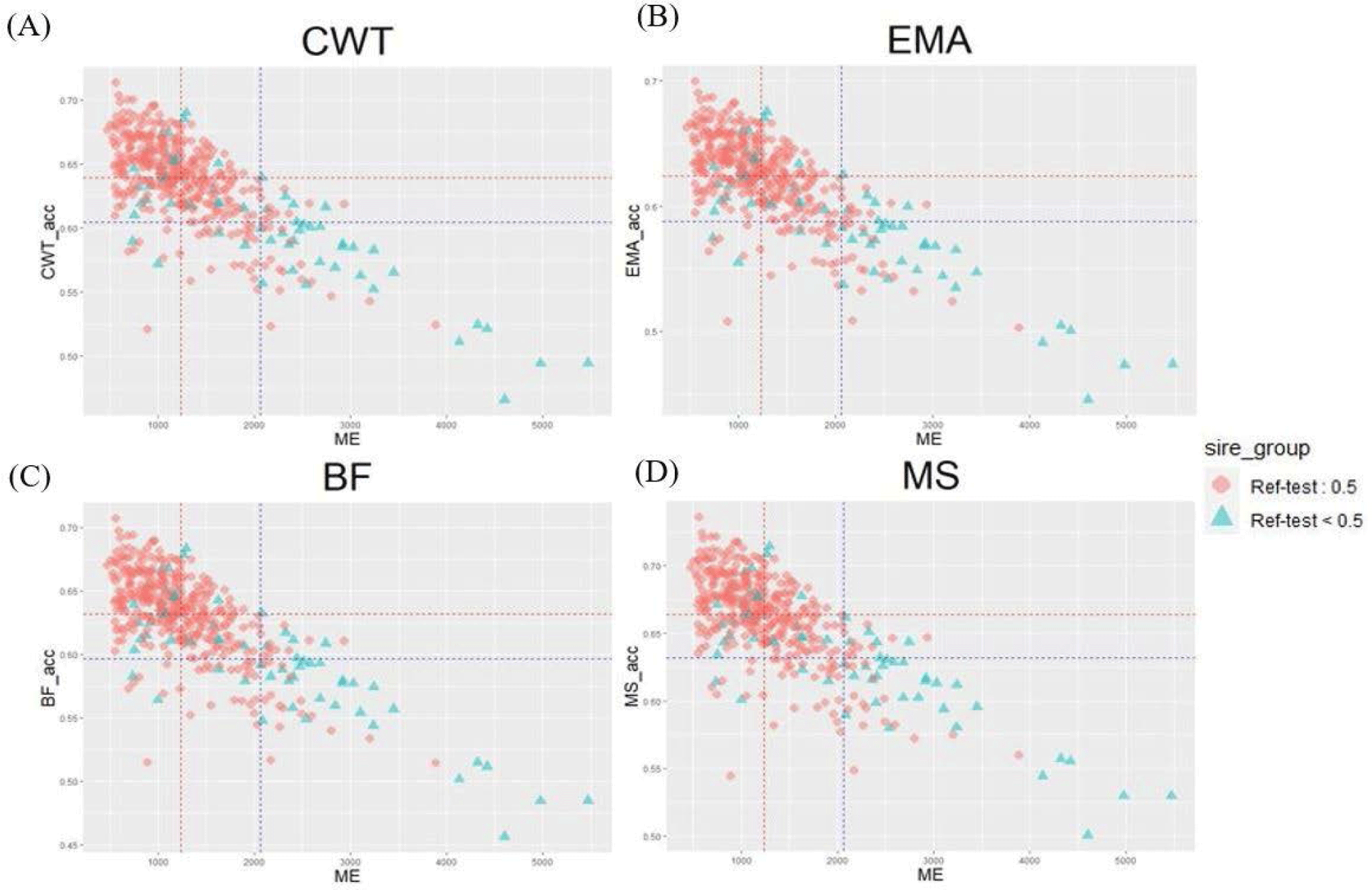
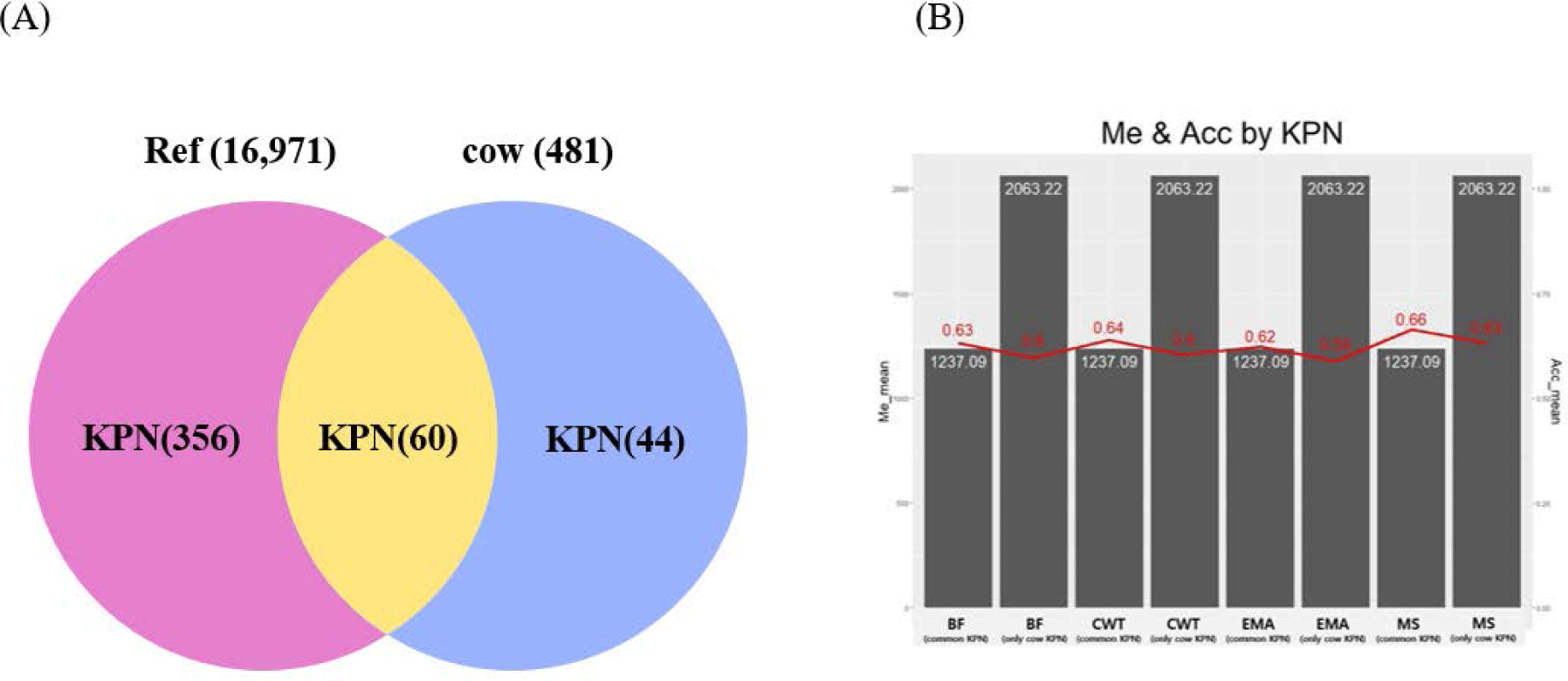
Genetic relatedness between reference and test populations is reflected in the M_e and effective population size (Ne) [34], where M_e represents the number of independent chromosomes arising during gametogenesis; the lower the M_e value, the closer the relationship between the reference and test populations [19]. Fig. 8 shows the correlation between the M_e values of the reference and test cow populations, and the accuracy of the EBVs for the 481 test cows. The correlations between the M_e values and accuracy values for CW, EMA, MS, and BFT were −0.74, −0.75, −0.73, and −0.75, respectively. The reference population included 356 KPN half-sibs and the replacement cow population consisted of 104 KPN half-sibs; 60 KPNs were common between the two populations (Fig. 9A). Fig. 9B shows the M_e values and accuracies of the EBVs of test cows with common KPN sires and different KPN ancestors. The M_e value of the common KPN cows was 1,237.09 for all traits, and the accuracies were 0.64, 0.62, 0.63, and 0.66 for CWT, EMA, BF, and MS, respectively. In contrast, the M_e value of the counterparts was 2,063.22 for all traits, and the accuracies were 0.6, 0.59, 0.6, and 0.63 for CWT, EMA, BF, and MS, respectively. It is logical to suggest that the closer genetic relationship between the reference and test animal (low M_e) led to more accurate EBV predictions. A set of simulation data was generated based on parameters with an Ne of 1,000, 51 quantitative trait loci (QTLs), and heritability of 0.3 to estimate the accuracy of the GBLUP method [35-37]. This simulation study showed that lower M_e (NQTL) values led to more accurate GBLUP and BayesB results. M_e is defined as the variance of identity by descent among individuals for genetic relatedness.

Fig. 8. Correlation between accuracy of genomic breeding value and number of effective chromosome segments (Me) in reference and test population all 4 traits (CWT, EMA, BFT and MS). Each line means the average value of accuracy and Me statistic. Red dots are cows with the same KPN between the reference and test population, blue dots are cows with only the KPN of the test population. CWT, carcass weight; EMA, eye muscle area; BFT, back-fat; MS, marbling score; KPN, Korea proven.

Download Original Figure

Fig. 9. Accuracy of test cow population with close relationship (0.25) and distinct relationship from reference population. (A) Pedigree structure for reference data set (Ref) and test data set (cow) which is share common ancestor (red: ancestor exist only reference data set, blue: ancestor exist only test data set, yellow: ancestor exist both reference and test data set). (B) Number of effective chromosome segment (Me) value and average EBV accuracy of test data set for all traits depend on the ancestor condition (common ancestor or only test data set ancestor). KPN, Korea proven; EBV, estimated breeding value.

Download Original Figure

In conclusion, we compared genomic prediction accuracy among three methods (PI, PBLUP, and GBLUP), using 258 KPN bulls with 95% accurate TBVs derived from BLUP. GBLUP outperformed PBLUP and the PI in terms of the accuracy of the EBVs. The accuracy of the GBLUP method was about 12% higher than that of the PBLUP method when using pedigree information. The accuracy of the GEBV method was higher than that of the PBLUP and PI for all traits, as reflected in cow EBVs estimated using collateral information (half-sib dataset). We propose that genomic data can be used to obtain random inheritance information about alleles from parents; this explains the high prediction accuracy of the GBLUP method used in this study. Moreover, genetic relatedness between the reference and test (cow) populations affected the accuracy of the EBVs estimated from the additive genetic relationship and M_e. A difference in M_e values between common KPN and cow KPN of about 820 increased the accuracy of the GBLUP by about 3.25%. Measuring the M_e value of animals could be useful for determining the accuracy of cow EBVs estimated using GBLUP.

Competing interests

No potential conflict of interest relevant to this article was reported.

Funding sources

The research funding was supported by HANWOOBOARD and partly supported by Korea Institute of Planning and Evaluation for Technology in Food, Agriculture, Forestry and Fisheries(IPET) funded by Ministry of Agriculture, Food and Rural Affairs(MAFRA)(321082-3).

Acknowledgements

The genotype dataset for cow validation (n=428) of EBV and large pedigree information (7 generation depth of pedigree) for estimating bull EBV was supported by the Korea Animal Improvement Association. Hyo-Sang Lee was a student at Artificial Intelligence Convergence Research Center of Chungnam National University. His financial support was supported by the Institute of Information & communications Technology Planning & evaluation (IITP) grant funded by the Korean government (MSIT) (No.2020-0-01441, Artificial Intelligence Convergence Research Center (Chungnam National University)).

Availability of data and material

Upon reasonable request, the datasets of this study can be available from the corresponding author.

Authors’ contributions

Conceptualization: Lee SH, Koo YM.

Data curation: Lee HS, Koo YM.

Formal analysis: Kim Y, Do CH.

Methodology: Lee HS, Kim Y, Lee KH.

Software and Validation: Lee DH, Seo D.

Investigation: Kim Y, Lee DJ.

Writing - original draft: Lee DH, Dinh PTN, Ekanayake W, Yoon D, Lee SH, Koo YM.

Writing - review & editing: Lee HS, Kim Y, Lee DH, Seo D, Lee DJ, Do CH, Dinh PTN, Ekanayake W, Lee KH, Yoon D, Lee SH, Koo YM.

Ethics approval and consent to participate

This article does not require IRB/IACUC approval because there are no human and animal participants.

REFERENCES

Chung KY, Lee SH, Cho SH, Kwon EG, Lee JH. Current situation and future prospects for beef production in South Korea — a review. Asian-Australas J Anim Sci. 2018; 31:951-60

Park B, Choi T, Kim S, Oh SH. National genetic evaluation (system) of Hanwoo (Korean native cattle). Asian-Australas J Anim Sci. 2013; 26:151-6

Peak BH. Overview of beef cattle (Hanwoo) production in Korea.In Proceedings of 2nd Korea-US-Japan International Joint Symposium. 2007College Station, TX.

Sun C, Madsen P, Nielsen US, Zhang Y, Lund MS, Su G. Comparison between a sire model and an animal model for genetic evaluation of fertility traits in Danish Holstein population. J Dairy Sci. 2009; 92:4063-71

Mehrban H, Lee DH, Naserkheil M, Moradi MH, Ibáñez-Escriche N. Comparison of conventional BLUP and single-step genomic BLUP evaluations for yearling weight and carcass traits in Hanwoo beef cattle using single trait and multi-trait models. PLOS ONE. 2019; 14e0223352

Nwogwugwu CP, Kim Y, Chung YJ, Jang SB, Roh SH, Kim S, et al. Effect of errors in pedigree on the accuracy of estimated breeding value for carcass traits in Korean Hanwoo cattle. Asian-Australas J Anim Sci. 2020; 33:1057-67

Henderson CR. Best linear unbiased estimation and prediction under a selection model. Biometrics. 1975; 31:423-47

Meuwissen THE, Hayes BJ, Goddard ME. Prediction of total genetic value using genome-wide dense marker maps. Genetics. 2001; 157:1819-29

Misztal I, Legarra A, Aguilar I. Computing procedures for genetic evaluation including phenotypic, full pedigree, and genomic information. J Dairy Sci. 2009; 92:4648-55

10.

Chen L, Schenkel F, Vinsky M, Crews DH, Li C. Accuracy of predicting genomic breeding values for residual feed intake in Angus and Charolais beef cattle. J Anim Sci. 2013; 91:4669-78

11.

Wolc A, Stricker C, Arango J, Settar P, Fulton JE, O’Sullivan NP, et al. Breeding value prediction for production traits in layer chickens using pedigree or genomic relationships in a reduced animal model. Genet Sel Evol. 2011; 43:5

12.

Nwogwugwu CP, Kim Y, Cho S, Roh HJ, Cha J, Lee SH, et al. Optimal population size to detect quantitative trait loci in Korean native chicken: a simulation study. Anim Biosci. 2022; 35:511-6

13.

Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007; 81:559-75

14.

Oldenbroek K, van der Waaij L. Textbook animal breeding: animal breeding and genetics for BSc students. Wageningen:: Centre for Genetic Resources and Animal Breeding and Genomics Group, Wageningen University and Research Centre. 2014

15.

Misztal I, Tsuruta S, Strabel T, Auvray B, Druet T, Lee DH. BLUPF90 and related programs (BGF90).In Proceedings of the 7th World Congress on Genetic Applied to Livestock Production. 2002 Montpellier, France.

16.

Misztal I, Tsuruta S, Lourenco D, Aguilar I, Legarra A, Vitezica Z. Manual for BLUPF90 family of programs. Athens:: University of Georgia. 2014

17.

Lee J, Cheng H, Garrick D, Golden B, Dekkers J, Park K, et al. Comparison of alternative approaches to single-trait genomic prediction using genotyped and non-genotyped Hanwoo beef cattle. Genet Sel Evol. 2017; 49:2

18.

VanRaden PM. Efficient methods to compute genomic predictions. J Dairy Sci. 2008; 91:4414-23

19.

Marjanovic J, Calus MPL. Factors affecting accuracy of estimated effective number of chromosome segments for numerically small breeds. J Anim Breed Genet. 2021; 138:151-60

20.

Goddard ME, Hayes BJ, Meuwissen THE. Using the genomic relationship matrix to predict the accuracy of genomic selection. J Anim Breed Genet. 2011; 128:409-21

21.

Martini JWR, Wimmer V, Erbe M, Simianer H. Epistasis and covariance: how gene interaction translates into genomic relationship. Theor Appl Genet. 2016; 129:963-76

22.

Jibrila I, ten Napel J, Vandenplas J, Veerkamp RF, Calus MPL. Investigating the impact of preselection on subsequent single-step genomic BLUP evaluation of preselected animals. Genet Sel Evol. 2020; 52:42

23.

Misztal I, Wiggans GR. Approximation of prediction error variance in large-scale animal models. J Dairy Sci. 1988; 71:27-32

24.

Harris B, Johnson D. Approximate reliability of genetic evaluations under an animal model. J Dairy Sci. 1998; 81:2723-8

25.

Mrode R. Linear models for the prediction of animal breeding values. 3rd ed. Wallingford, Oxfordshire: CABI. 2014

26.

Naserkheil M, Lee DH, Mehrban H. Improving the accuracy of genomic evaluation for linear body measurement traits using single-step genomic best linear unbiased prediction in Hanwoo beef cattle. BMC Genet. 2020; 21:144

27.

Kim EH, Kang HC, Sun DW, Myung CH, Kim JY, Lee DH, et al. Estimation of breeding value and accuracy using pedigree and genotype of Hanwoo cows (Korean cattle). J Anim Breed Genet. 2022; 139:281-91

28.

Bangera R, Correa K, Lhorente JP, Figueroa R, Yáñez JM. Genomic predictions can accelerate selection for resistance against Piscirickettsia salmonis in Atlantic salmon (Salmo salar). BMC Genomics. 2017; 18:121

29.

Clark SA, Hickey JM, Daetwyler HD, van der Werf JHJ. The importance of information on relatives for the prediction of genomic breeding values and the implications for the makeup of reference data sets in livestock breeding schemes. Genet Sel Evol. 2012; 44:4

30.

Hayes BJ, Visscher PM, Goddard ME. Increased accuracy of artificial selection by using the realized relationship matrix. Genet Res. 2009; 91:47-60

31.

Habier D, Fernando RL, Dekkers JCM. The impact of genetic relationship information on genome-assisted breeding values. Genetics. 2007; 177:2389-97

32.

Habier D, Tetens J, Seefried FR, Lichtner P, Thaller G. The impact of genetic relationship information on genomic breeding values in German Holstein cattle. Genet Sel Evol. 2010; 42:5

33.

Daetwyler HD, Villanueva B, Bijma P, Woolliams JA. Inbreeding in genome-wide selection. J Anim Breed Genet. 2007; 124:369-76

34.

Lee SH, Clark S, van der Werf JHJ. Estimation of genomic prediction accuracy from reference populations with varying degrees of relationship. PLOS ONE. 2017; 12e0189775

35.

Zhang X, Lourenco D, Aguilar I, Legarra A, Misztal I. Weighting strategies for single-step genomic BLUP: an iterative approach for accurate calculation of GEBV and GWAS. Front Genet. 2016; 7:151

36.

Daetwyler HD, Pong-Wong R, Villanueva B, Woolliams JA. The impact of genetic architecture on genome-wide evaluation methods. Genetics. 2010; 185:1021-31

37.

Clark SA, Hickey JM, van der Werf JHJ. Different models of genetic variation and their effect on genomic evaluation. Genet Sel Evol. 2011; 43:18

Related Articles

Comparison of accuracy of breeding value for cow from three methods in Hanwoo (Korean cattle) population

Abstract

INTRODUCTION

MATERIALS AND METHODS

RESULTS AND DISCUSSION

Competing interests

Funding sources

Acknowledgements

Availability of data and material

Authors’ contributions

Ethics approval and consent to participate

REFERENCES