INTRODUCTION
In the Korea, whole crop maize (Zea mays L.; WCM) and soybeans account for 60% of total feedstock use, and its self-sufficiency rate is around 1%. Therefore, a large proportion of the ingredients in feedstock need to be imported [1]. As the main silage resource in the Korea, WCM cultivation area totals 13,000 ha, and the amount produced was 228,000 tons in 2018 (28.79% of the total summer forage crop), according to annual statistics of forage supply of the Rural Development Administration (RDA). The self-sufficiency rate of high quality-forage is not as high as that of dairy farming and stands at less than 30% due to the weak base of forage production. In counties with a high dependency on imports, such as the Korea, it is important to be able to predict forage production to ensure flexibility between domestic production and importation.
Various environmental factors contribute to high WCM production including weather, soil type, pests, diseases, and farm-management practices [2]. The most important factors are climatic factors such as temperature and available moisture during key physiological growing periods [3]. In Korea, high rainfall in the Changma (Korean monsoon) season exceeding the appropriate level required for growth had a negative impact on WCM production [4,5]. The impact of heavy rainfall (deemed an abnormal climate event) was critical to the trend in WCM production each year. As a result, the forecasted production of WCM in 2045 decreased to 70% of the production in 2015 due to the increasing frequency and intensity of these events [6]. While these studies were able to easily interpret the effects these events had on production, they were unable to reflect the complex relationships between different climate variables as part of the natural ecosystem.
Since the 1990s, various models have been developed to predict crop production and/or productivity. Examples of these are the decision support system for agro-technology transfer; the cropping system model (DSSA-CSM) which includes soil, crop, climate and management; the crop simulation models (CSM) which includes soil condition, weather and management practices; and the agricultural production system simulator (APSIM) which includes many economic, biological, and environmental modules [7–9]. These systems are all able to precisely calculate production/productivity, however, it is still difficult to explain how the relationship between these variables might affect the results like a black-box [10]. Therefore, it is necessary to study structuralized causality by considering the various climatic factors as part of the natural ecosystem.
In general, a cause-and-effect relationship refers to a direct relationship between a single cause and a single effect. In this study, causality was defined as a characteristic of a network consisting of many cause-and-effect relationships. Therefore, causality in complex structures, which include both direct and indirect relationships, should be distinguished from the cause-and-effect relationship seen in simple structures. Furthermore, causality was generated by analyzing the relationship between various causes, mediators and effects [11]. Structural equation modeling (SEM) is a statistical technique that identifies causality between different factors and consists of two parts: The measurement part where common characteristics are extracted to generate common factors from the variables, and a structural part where connections are set between the extracted common factors [12]. This process creates a big network where balance needs to be kept between the high degree of model fitness and the parsimony to allow for easy interpretation. There is a clear relationship between agricultural climatic factors and crop production, therefore, it is advantageous to form a causality network to estimate the effects each climatic factor has on crop production.
In agricultural sciences, SEM is a useful tool for understanding the causal relationship between crop production and environmental factors [13]. In terms of cultivation management, the paths of irrigation and planting density stood out as key factors for Cleistogenes songorica yield [14]. Zhang et al. [15] reported that early-season vigor, plant height, seed weight, number of bolls/area and boll weight all had effects on Canadian flax yield by using SEM. In Korean agricultural sciences, the seasonal effects of climatic factors between the autumn and spring growing periods on the production of Italian ryegrass were remarkable [16]. Furthermore, the indirect effects of precipitation, temperature and soil properties were notable in the paddy fields [17]. Additionally, when comparing climatic causality between paddy fields and upland fields, the production of Italian ryegrass in the paddy fields was sensitive to temperature due to the short growing period caused by the rice-winter crop rotation system [18]. Studies on the causal relationship between climate and crop production were also carried out for forage barley [19] and forage rye [20]. Winter is an important season for survival for these winter forage crops. Therefore, the growing period is naturally divided into the periods of autumn and the following spring.
On the other hand, for summer forage crops, it is difficult to classify their growing periods by season due to continuity of growth and development across seasons. In this study, the longitudinal characteristics were considered by taking into account the crop’s growth stage instead of which season it was. In general, the growth stages of WCM have divided into two stages: the vegetative stage and the reproductive stage; where the reproductive stage starts after the silking stage [21]. This silking stage is important since this is when kernel fertilization, support ear weight and kernel fill are all determined. Furthermore, climatic conditions during the stage of 50% silking are critical to the yield and quality of WCM [3]. Therefore, for WCM, the longitudinal characteristics were determined before and after the silking stage.
The important point of this study was to estimate the various impacts of climatic factors on WCM production by considering the major silking stage of the growth stages under a network that assumes a part of the natural ecosystem, unlike other studies that considered a simple cause-and-effect relationship. Therefore, this study aimed to assess the causality of climatic factors based on temperature, rainfall, humidity, wind and sunshine on WCM production using SEM by looking at the stages before and after silking. In addition, for the estimated major causality, it was identified which range of climatic factors directly or indirectly affect production.
MATERIALS AND METHODS
The raw WCM data (n = 993) which includes dry matter yield (DMY, kg/ha), fresh matter yield (FMY, kg/ha), total digestible nutrients yield (TDNY, kg/ha), year, location, seeding date, silking date and harvesting date were collected from the reports of new variety adaptability of the Rural Development Administration (RDA) for 1985–2011 as metadata. For the homogeneity of data, the central inland region (n = 656) was selected according to the classification criteria of Ko et al. [22]; where, Cheonan (36°48’N, 127°9’E), Icheon (37°16’N, 127°26’E) and Suwon (37°17’N, 127°0’E) all belong to the central inland region.
Climate data for the WCM metadata were collected from the weather information systems of the Korean Meteorological Administration (KMA). This data included daily temperature, rainfall, wind speed and sunshine duration and was categorized by year and location. The climate information was matched based on cultivation location and year of cultivation via open-application programming interface (API). Cases (n = 16) where information was inconsistent due to missing seeding and/or harvesting dates were eliminated. This resulted in a final dataset (n = 640) being used to construct a structure of causality for different climatic factors affecting WCM production.
The following climate variables were generated for the seeding‒silking (SS) stage and silking‒harvesting (SH) stage as follows: growing degree days over 10°C (SSGDD and SHGDD, °C), highest temperature (SSHT and SHHT, °C), lowest temperature (SSLT and SHLT, °C), soil surface temperature (SSST and SHST, °C), relative humidity (SSRH and SHRH, %), total rainfall (SSRA and SHRA, mm), wind speed (SSWS and SHWS, m/s), total sunshine duration (SSSD and SHSD, hr). All climate variables (except SSRA, SHRA, SSSD, and SHSD which were calculated as sums over the whole growing stage) were calculated as daily means over the growing stage.
The following procedure was used to assess the causality of different climatic factors one WCM production: Firstly, climate variables were compared to check for seasonal effects between the SS and SH stages by using a paired t-test with a 5% significance level. Secondly, because there were various climate variables, it was necessary to check the association between them using correlation analysis. Next, the structure for causality for the different climate variables was constructed and assessed using SEM. Finally, the climatic variables that had the biggest effect on production at each stage of growth were selected and their relationships were illustrated.
In this study, SEM consisted of a measurement part that extracted common factors from various climate variables and a structural part where connections are set between the extracted common factors [11]. The equation for the measurement part is as follows:
where variables consist of climate variables in the SS stage (XSS = (SSGDD,SSHT,SSLT,SSST,SSRH,SSRA,SSWS,SSSD)T), climate variables in the SH stage (XSH = (SHGDD,SHHT,SHLT,SHST,SHRH,SHRA,SHWS,SHSD)T) and production (Y = (FMY,DMY,TDNY)T). For the common factor , ηSS, ηSH and ξ were climatic factors in the SS stage, climatic factor in SH stage and production factor, respectively. Ʌ is a parameter matrix, which indicates an association between variables and common factors. δ is a residual in the measurement part. D is the relationship of residuals before and after the silking stage, which indicates that the structure to model the interaction between residuals is a vector of pseudo-factors [23]. The structural part which reflects causality between the climatic variables and production was as follows:
where B and T are coefficients of pathways between climatic factors and coefficients of pathways between production and climatic factors, respectively. ε is the residual in the structural part. The pathways that had effects on production were selected using a 5% significance level, and their direction was set using meteorological evidence and logic. In particular, η is located on both the left and right sides in SEM, which indicates it can be used to connect two or more cause-and-effect relationships, unlike models with a single response variable [11]. Some subset of η is the result in the preceding relationship, and at the same time, it is the effect in the subsequent relationship. In SEM, it was necessary to evaluate model fitness and model parsimony. In this study, the goodness of fit index (GFI) and comparative fit index (CFI) were used to evaluate model fitness, and parsimony GFI (PGFI) and parsimony CFI (PCFI) were used to evaluate model parsimony.
Paired t-test, correlation analysis and factor analysis were performed using SPSS 24.0 (IBM, Chicago, IL, USA), and SEM was performed using AMOS 24.0 (IBM) and visualization was performed using “plot3D” package of R 3.6.0.
RESULTS AND DISCUSSION
The characteristics of WCM production and climate variables for the central inland region of Korea are illustrated in Table 1. Furthermore, the longitudinal characteristics of the climate variables between the SS and SH stages using a paired t-test are described in Table 2. For the production of WCM, FMY, DMY and TDNY were 56,298, 16,149, and 11,399 kg/ha, respectively. Therefore, DM and TDN percentages were 28.68% and 70.59%, respectively. The growing periods of the SS and SH stages were 78 days and 38 days, respectively. In general, silking occurred in mid-late July overlapping the heatwave that hits the Korean Peninsula each year at the end of Changma season [24, 25]. Therefore, the mean temperatures (SHHT, SHLT, and SHST) in the SH stage were higher than those (SSHT, SSLT, and SSST) in the SS stage (p < 0.05). Meanwhile, SSGDD was higher than SHGDD (p < 0.05) because of a much longer growing period (78 days vs. 38 days), even though the temperature was higher in the SH stage. Due to heavy rainfall in the Changma season, SHRA and SHRH were higher than SSRA and SSRH, respectively (p < 0.05). In particular, maximum SHRA was 1,340.80 mm, indicating a high probability of soil erosion based on 1,000–1,400 mm of rainfall being the average annual rainfall for the central regions of Korea [26]. In the case of wind speed (m/s), SSWS and SHWS were 1.84 and 1.86, respectively (p < 0.05). However, longitudinal difference between SSWS and SHWS showed no significance (p = 0.24). According to Moon and Choi [27], typhoons actively approach the Korean Peninsula in July and August, however, the typhoons in July come without rainfall, whereas the typhoons in August are accompanied by heavy rainfall. Therefore, not only does the Changma season bring concentrated rainfall, but it also has typhoons that bring heavy rainfall. This is why there is a difference between SSRA and SHRA but not between SSWS and SHWS. Finally, SSSD and SHSD were 232.19 and 147.32 hr, respectively (p < 0.05). This implies that sunshine duration was shorter due to the shorter growing period and/or longer rainy days in the SH stage. In summary, the differences in longitudinal characteristics between before and after the silking stages were obvious for all the climate variables (except wind speed).
In general, climate variables are not independent of each other with regard to their effect on crop production [5]. Therefore, it was necessary to check climate variable association within and between growth stages using the correlation coefficient (Table 3). Based on a correlation coefficient (|r| > 0.4), the positive associations of SSST and SSLT, SSST and SSHT and negative associations of SSSD and SSRA were confirmed within the SS stage (p < 0.05). Within the SH stage, SHST was positively associated with SHHT, SHLT, and SHSD (p < 0.05). Between the SS stage and SH stage, the longitudinal self-associations were prominent in GDD, ST, and RH (p < 0.05). These associations between climate variables were used to construct the structure of the SEM.
SSGDD, seeding-silking growing degree days; SSHT, seeding-silking high temperature; SSLT, seeding-silking low temperature; SSST, seeding-silking soil surface temperature; SSRH, seeding-silking relative humidity; SSRA, seeding-silking rainfall amount; SSWS, seeding-silking wind speed; SSSD, seeding-silking sunshine duration; SHGDD, silking-harvesting growing degree days; SHHT, silking-harvesting high temperature; SHLT, silking-harvesting low temperature; SHST, silking-harvesting soil surface temperature; SHRH, silking-harvesting relative humidity; SHRA, silking-harvesting rainfall amount; SHWS, silking-harvesting wind speed; SHSD, silking-harvesting sunshine duration.
In addition to the associations between climate variables, the effects of climate variables on WCM production were important in determining the path direction and structure of SEM. Using step-wise selection of the regression model (Table 4), the selected variables that affected production were SSGDD, SSHT, SSST, SSRA, SSWS, SSSD, SHGDD, SHST, and SHRA for DMY of WCM (p < 0.05); where, SSGDD, SSST, SSRA, SSSD, SHGDD, and SHST had positive effects; and SSHT, SSWS and SHRH had negative effects, respectively. In particular, under the condition of no multicollinearity (variance inflation factor [VIF] < 4), the negative effect of SSHT was questionable. Furthermore, the opposing effects of SSRA and SHRA were noticeable. However, it is inappropriate to directly interpret these effects, therefore, it should be checked in the flow of causality for the different climate variables.
Firstly, to establish a structure of causality, it was necessary to identify the commonality between climate variables during the measurement part of SEM (Table 5); where the strength of commonality was based on factor lodging scores (|factor lodging| > 0.6). In the SS stage, the first factor was strongly related to positive SSRA and negative SSSD, which is characteristic of rain. The second factor was associated with positive SSHT, positive SSRH and negative SSWS, which is characteristic of heat-humidity. The final factor was related to positive SSGDD, positive SSLT and positive SSST, which has the characteristics of the temperatures needed for growth and development. In the SH stage, the first factor was strongly related to positive SHLT and positive SHWS (|factor lodging| > 0.7), which indicates a tropical night (daily lowest temperature was recorded at night). The second factor was related to positive SHGDD, positive SHHT, positive SHST and positive SHSD, which has the characteristics of the temperatures needed for growth and development. The last factor was related to positive SHRH and positive SHRA, which was characteristic of rain. These factors were arranged in order of importance based on the sum of factor lodging, which represents the rate at which the factor contributes when all variables form a 100% contribution rate [28]. Furthermore, the cumulated lodgings (%) in the SS and SH stages were 71.19 and 70.20, respectively, indicating that the loss of information by reduction from variable to factor was less than 30%. It was hypothesized that the negative effect of SSHT on DMY was caused by heat-humidity related stress in the SS stage, which was assessed by SEM.
Six climatic factors were named: Rainfall_SS, Heat-humidity_SS, Temperature_SS, and Night-heat_SH, Temperature_SH and Rainfall_SH. In addition to climatic factors, the production factor consisting of FMY, DMY, and TDNY was used as the final response factor. Here, it was necessary to evaluate physiological/ecological evidence to set the path’s direction between factors. There was no doubt in setting the direction of climatic factors from before to after because of the time series feature. The path between changes in temperature leading to changes in rainfall can be explained through a long-term mechanism which starts with a temperature rise, and is followed by atmospheric and soil surface moisture evaporation, moisture condensation in the atmosphere, and ends with rainfall [29]. On the other hand, the path between changes in rainfall leading to changes in temperature can be illustrated by controlling the divide between the sensible and latent heat fluxes over a relatively short period of time [30]. Therefore, in this study, daily meteorological information was used and concluded that the path from changes in rainfall to changes in temperature was appropriate. Furthermore, for winter forage crops, the cause-and-effect relationship between temperature and precipitation in the causality network was constructed following the path of changes in rainfall to changes in temperature [16–20]. Finally, for the stress factors within each stage, the path was explored under the condition of no distortion to other factors.
As a result, the structure for the causality of climate variables affecting WCM production was established as shown in Fig. 1. In equation (1), the structure part was as follows:
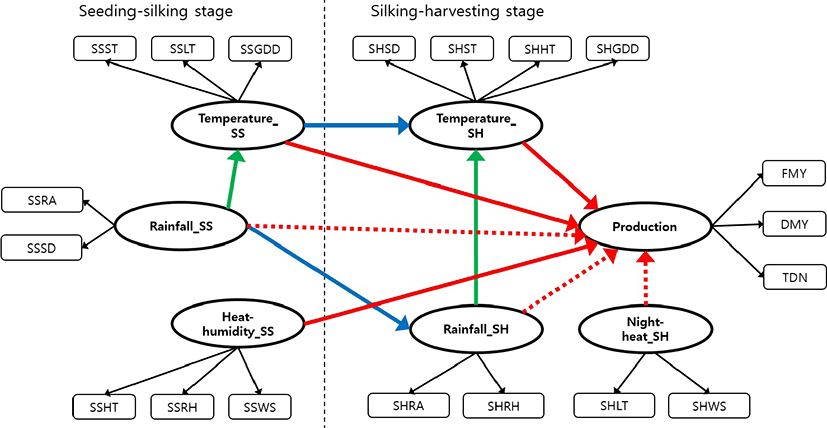
were η1, η2, η3, and η4 Temperature_SS, Temperature_SH, Rainfall_SH and Production, respectively. These were response factors in causality at least once. In particular, η4 was the final response factor affected by all factors. ξ1, ξ2, and ξ3 were Rainfall_SS, Heat-humidity_SS and Night heat_SH, respectively. These were factors that marked the beginning of each path that constitutes a causality.
There were three key cause-and-effect relationships: The first was the direct effect of climatic factors on the production of WCM (red-colored). The paths of Temperature_SS, Temperature_SH and Heat-humidity_SS had effects on WCM production (p < 0.05). In the case of the insignificant paths (red-colored dash line), the impact of Night-heat_SH on WCM production was not serious because SHLT in Korea was in range of 15.15°C‒21.15°C, it was not at the level to inhibit the growth of WCM. Here, the night temperatures of 70℉‒80℉ (21.11°C‒26.67°C) can affect the yield potential of WCM [31]. Meanwhile, in the case of Rainfall_SS and Rainfall_SH, the indirect path affected WCM production through two or more paths, while their direct path was not affected. The second key cause-and-effect relationship was the indirect effect of different pathways within the growth stage (green colored). Regardless of the growth stage, rainfall only affected production in connection with the path of temperature, not direct path. Therefore, it was hypothesized that the rainfall does not directly affect production, but rather affects production through a certain temperature. The final key cause-and-effect relationship was the seasonal effects between the SS and SH stages on the longitudinal structure for temperature and rainfall related climatic factors (blue colored). Thus, the effects of the different temperature and rainfall related factors during the SS stage could be categorized into direct and indirect seasonal effects.
To assess causality, all paths in the structure were estimated with a 5% significance level as illustrated in Table 6. In the structural part, causality could be identified along the routes consisting of pathways for the various cause-and-effect relationships between the climatic factors. For example, in the case of Rainfall_SS, its effects led to changes in production through three routes. Firstly, the shortest route, ‘Rainfall_SS → Temperature_SS → Production’, was through a single mediate factor. Secondly, the route, ‘Rainfall_SS → Temperature_SS → Temperature_SH → Production’, consisted of a pathway that reflects the seasonal effect of temperature. Finally, the route, ‘Rainfall_SS → Rainfall_SH → Temperature_SH → Production’, consisted of a pathway that reflects the seasonal effect of rainfall. Hence, the total effect of Rainfall_SS was 32.96 (=0.01 × 2,622.64 + 0.01 × 54.91 × 14.79 + 0.36 × (−0.26) × 14.79). The first rout indicates that the temperature and rainfall-based growth and development in the SS stage had a direct effect on the WCM production, regardless of them in the SH stage. The second route focused on the impact of temperature in the SH stage, which implies that the growth and development in the SS stage affected the production indirectly through the temperature. The final route also focused on the impact of temperature in the SH stage, but indicates that the WCM production was influenced by the seasonal effect of rainfall between the SS and SH stages, unlike the second route.
DMY, dry matter yield; FMY, fresh matter yield; TDNY, total digestible nutrients yield; SS, seeding-silking; SSSD, seeding-silking sunshine duration; SSRA, seeding-silking rainfall amount; SSWS, seeding-silking wind speed; SSHT, seeding-silking high temperature; SSRH seeding-silking relative humidity; SSST, seeding-silking soil surface temperature; SSGDD, seeding-silking growing degree days; SSLT, seeding-silking low temperature; SH, silking-harvesting; SHSD, silking-harvesting sunshine duration; SHGDD, silking-harvesting growing degree days; SHHT, silking-harvesting high temperature; SHST, silking-harvesting soil surface temperature; SHRA, silking-harvesting rainfall amount; SHRH, silking–harvesting relative humidity.
Under the causality network, the effect of climatic factors on WCM production through various pathways was determined by categorizing them into direct and indirect effects. For the causality between different climatic factors, the temperature in the SH stage was the most important mediate object for processes where other factors affected production. To compare the total effect between different climatic factors, the standardized total effect was calculated by using a standardized weight. The standardized total effect was greatest in the following order based on the absolute value: Temperature_SS (0.16), Rainfall_SS (0.15), Temperature_SH (0.13), Heat-humidity_SS (−0.09) and Rainfall_SH (−0.06); where the greater the absolute value, the more sensitive WCM production is to that particular climatic factor. The climatic factors in the SS stage were more important than those in the SH stage. Furthermore, regardless of the growth stage, WCM production was more sensitive to temperature than rainfall. In particular, the effect of rainfall before and after the silking stage was markedly different. In general, WCM produces high DMY and therefore has a high requirement for nutrients especially nitrogen (N), phosphorus (P) and potassium (K) in silking stage. The period of highest fertilizer requirement for N was from 1 week before to 3 weeks after, P from 3 weeks before to 3 weeks after, and K from 4 weeks after silking. At this time, temperature and sunshine duration were important to promote soil fertilizer composition and photosynthesis [32]. At this period, it is likely that WCM is lodged by rainfall with wind because of the rapid growth of stalk compared to the development and settlement of roots. In particular, except for 15 days before silking, DMY was decreased by root lodging [33]. Furthermore, as the stage progressed, the reduction in net assimilation rate increased, with more by stalk lodging than by root lodging. In this study, although weather events such as heavy rain and typhoons did not appear as stressors in the SH stage, but based on the negative impact of Rainfall_SH, it was hypothesized that excessive rainfall had an effect on the reduction in WCM production.
In general, explaining which variables had the largest effect is difficult as estimation are being performed using a factor score, although SEM did determine the flow and structure of causality. Hence, for the major causality between climate and WCM production factors, it was necessary to select the main variables that would help to interpret in terms of physiology and ecology.
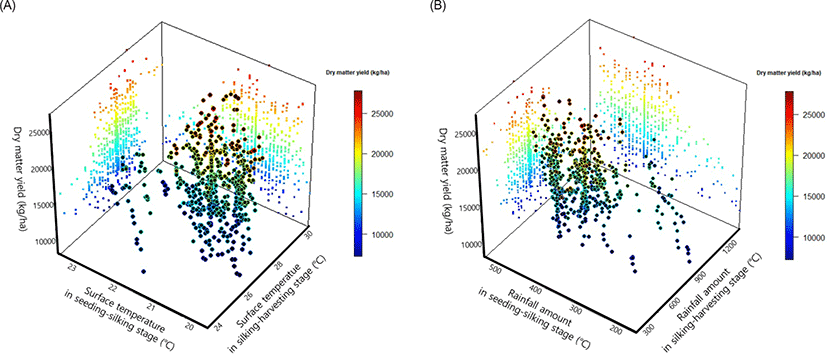
In this study, the major causality was found in the cause-and-effect relationships of temperature and rainfall between/within the SS and SH stages. Based on the results of factor analysis and correlation analysis, SSST, SHST, SSRA, SHRA, and DMY were selected (the main climate variables) as being representative of Temperature_SS, Temperature_SH, Rainfall_SS, Rainfall_SH, and production factors, respectively. The effect of SSST, SHST, SSRA, and SHRA on DMY of WCM within and between the growth stages is shown in Figs. 2 and 3, respectively. The association between the two variables and DMY was identified through the flow, which consisted of the direct and indirect effects found using SEM. Therefore, their effect could be explained through the flow of cause-and-effect rather than occurring at the same time.
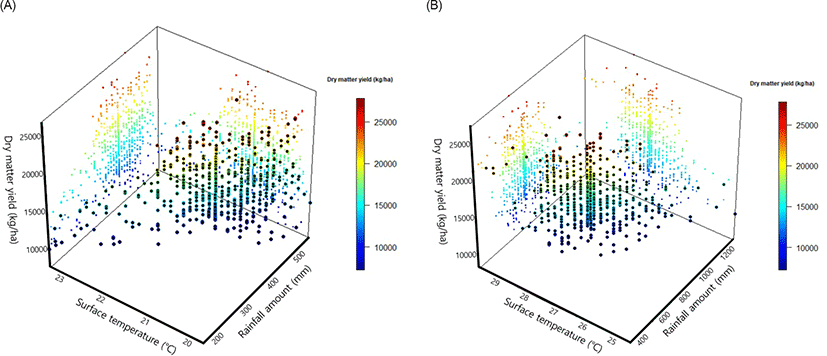
During the SS stage, high DMY occurred when SSST was less than 22°C and SSRA was over 300 mm (Fig. 2A). This implies that the indirect effect of SSRA occurred through a certain range of SSST (20°C‒22°C) based on the structure of SEM in this study. Furthermore, within this range of SSST, the variation in SSRA was larger. During the SH stage, the high DMY occurred when SHST was in the 26.5°C‒29.7°C region and SHRA was less than 900 mm (Fig. 2B), which indicates that the indirect effect of SHRA being below 900 mm led to higher DMY when SHST was also higher. According to Willis et al. [34], the optimum soil temperature was 23.89°C at a depth of 10.16 cm for WCM growth in central IOWA (40°36’N‒43°30’N). Therefore, SSST was a normal level for the growth and development of WCM, whilst SHST was higher. However, while SHST was somewhat higher, it was not at a level that would be concerning for growth as it was still less than the maximum temperature (30°C) of growing degree days for WCM. In the case of SSRA and SHRA, the appropriate rainfall amount for the growth and development of WCM was 450‒600 mm [35]. Furthermore, rainfall that can cause soil erosion is more of a problem when over 200 mm of concentrated rain falls in less than 3 months compared to over 1,000 mm of rain falling over a 12 month period, even when assuming the same amount of monthly rainfall [36]. In this study, areas with either low rainfall in the SS stage or excessive rainfall in the SH stage were found to have low DMY with small variations. In the late 21st century, annual rainfall is expected to increase by 30% in the Korean Peninsula [37]; therefore, there is a concern that production damage of summer crops will gradually increase due to excessive rainfall during the SH stage with overlapping the Changma season.
For the seasonal effect of temperature (Fig. 3A), the variation of SSST below 22°C mostly led to the variation of SHST in the range of 26°C‒30°C. Furthermore, DMY showed a tendency to increase with increasing SHST. This means that for DMY of WCM (which consists of leaves, stems and grains), the growth and development of leaves and stems during the vegetative stage continued through to the reproductive stage. Moreover, the growth of the grain in the reproductive stage caused by increasing SHST led to increases in DMY. For the seasonal effect of rainfall (Fig. 3B), high DMY was rarely recorded in the areas where SSRA was below 300 mm, and when SSRA was above 300 mm, high DMY was found when SHRA was 600‒900 mm. In particular, it was determined that there was few red dots indicating that the high DMY when SHRA was above 1,000 mm. Kim et al. [6] reported that the WCM yield is damaged by heavy rainfall (7.6 mm hour−1 and 1,000 mm in July). Although the excessive rainfall was not determined as stress factor in the SH stage in this study, it was reflected into the negative effects of SHRA on WCM production.
In summary, for the causality of soil surface temperature and rainfall during the SS and SH stages, rainfall can be effective to an increase in DMY only through an increase in temperature when it was in a certain range. Furthermore, seasonal effects led to more pronounced causality in the SH stage than in the SS stage. Unfortunately, this study was not able to confirm causality based on the growth and development of WCM in stages other than the silking stage. Furthermore, there was a drawback that only the climatic factor was considered among the various factors expected to affect WCM production. Thus, in the future, the causality network will be expanded to represent a more sophisticated flow by reflecting specific seasons and/or growth stages. As a follow-up study, we plan to expand the structure of causality for WCM production by taking into account soil physical properties, such as slope, drainage class and effective soil depth.
CONCLUSION
In this study, the causality of climate variables before and after the silking stage was assessed for the production of WCM using SEM which contained various cause-and-effect relationships. This study noted three key factors: the seasonal effect before and after the silking stage, the indirect effect of rainfall based on appropriate temperature, and the stressor caused by heat-humidity before the silking stage. Furthermore, it has been found that only a certain range of rainfall (above 30 mm in the before silking, 600‒900 mm in the after silking) affected WCM production when the temperature was appropriate before and after or within the silking stage for the major causality.
















